判断二分图

难度: Medium

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。

给定一个二维数组 graph ，表示图，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

不存在自环（graph[u] 不包含 u）。
不存在平行边（graph[u] 不包含重复值）。
如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例 1：

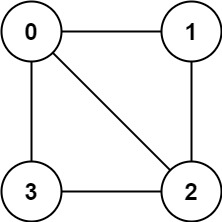
输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

示例 2：

输入：graph = [[1,3],[0,2],[1,3],[0,2]]
输出：true
解释：可以将节点分成两组: {0, 2} 和 {1, 3} 。

提示：

graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] 不会包含 u
graph[u] 的所有值 互不相同
如果 graph[u] 包含 v，那么 graph[v] 也会包含 u

注意：本题与主站 785 题相同： https://leetcode-cn.com/problems/is-graph-bipartite/

Submission

运行时间: 24 ms

内存: 16.5 MB

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        l = len(graph)
        s = [0] * l
        for i in range(l):
            if not s[i]:
                s[i] = 1
                queue = deque([i])
                while queue:
                    now = queue.popleft()
                    for j in graph[now]:
                        if s[now] == s[j]:
                            return False
                        elif not s[j]:
                            s[j] = -s[now]
                            queue.append(j)
        return True

Explain

此题解采用了广度优先搜索（BFS）来判断一个图是否是二分图。首先，创建一个长度与节点数相同的数组 s 来记录每个节点的颜色（使用 1 和 -1 表示两种不同的颜色），初始化为 0 表示未涂色。遍历每个节点，如果节点未被涂色，则将其涂色为 1 并将其加入队列中。在 BFS 过程中，从队列中取出节点 now，检查其所有邻接节点。如果邻接节点已经涂色且颜色与当前节点相同，则图不能被二分，返回 false。如果邻接节点未涂色，则将其涂成与当前节点相反的颜色并加入队列。如果所有节点都被正确涂色，说明图是二分图，返回 true。

时间复杂度: O(V + E)

空间复杂度: O(V)

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        l = len(graph)  # 图的节点数
        s = [0] * l  # 存储节点颜色，0为未涂色，1和-1为两种颜色
        for i in range(l):  # 遍历所有节点
            if not s[i]:  # 如果节点未涂色
                s[i] = 1  # 初始涂色为1
                queue = deque([i])  # 使用队列进行BFS
                while queue:
                    now = queue.popleft()  # 取出当前节点
                    for j in graph[now]:  # 遍历当前节点的所有邻接节点
                        if s[now] == s[j]:  # 如果邻接节点已涂色且颜色与当前节点相同
                            return False  # 不能二分，返回false
                        elif not s[j]:  # 如果邻接节点未涂色
                            s[j] = -s[now]  # 涂成相反颜色
                            queue.append(j)  # 加入队列继续BFS
        return True  # 所有节点处理完毕，是二分图

Explore

在二分图的定义中，图的所有顶点可以被分成两个不相交的集合，使得图中每条边的两个顶点分别属于这两个集合。因此，只需要两种颜色来区分是否可以将顶点分到这两个集合中。使用两种颜色的方法是直接和简洁的，符合二分图性质的要求。如果使用更多的颜色或其他复杂的标记方法，并不会提供额外的帮助，反而可能增加理解和实现的复杂度。

实际上，题解中的方法已经是在涂色过程中尽可能早地检测冲突。当我们为一个节点涂色时，我们会立即检查其所有邻接节点。一旦发现任何邻接节点已经涂色且颜色与当前节点相同，算法会立即返回false，因此这已经是一种效率较高的检测方式。进一步的优化可能涉及更细节的实现技巧，但在涂色和检测的逻辑上，当前的方法已经尽可能早地进行了冲突检测。

在非连通图中，可能存在多个独立的子图。题解中通过遍历每个节点并检查其是否已被涂色，确保了每个独立子图都会从某个未涂色的节点开始进行BFS。这种方式可以保证每个子图都被初始化并检查其是否可以二分。因为每个子图都是独立处理的，所以不会互相影响，从而确保了整个图的每个部分都被正确地判断。这是处理非连通图判断二分性的标准和有效方法。