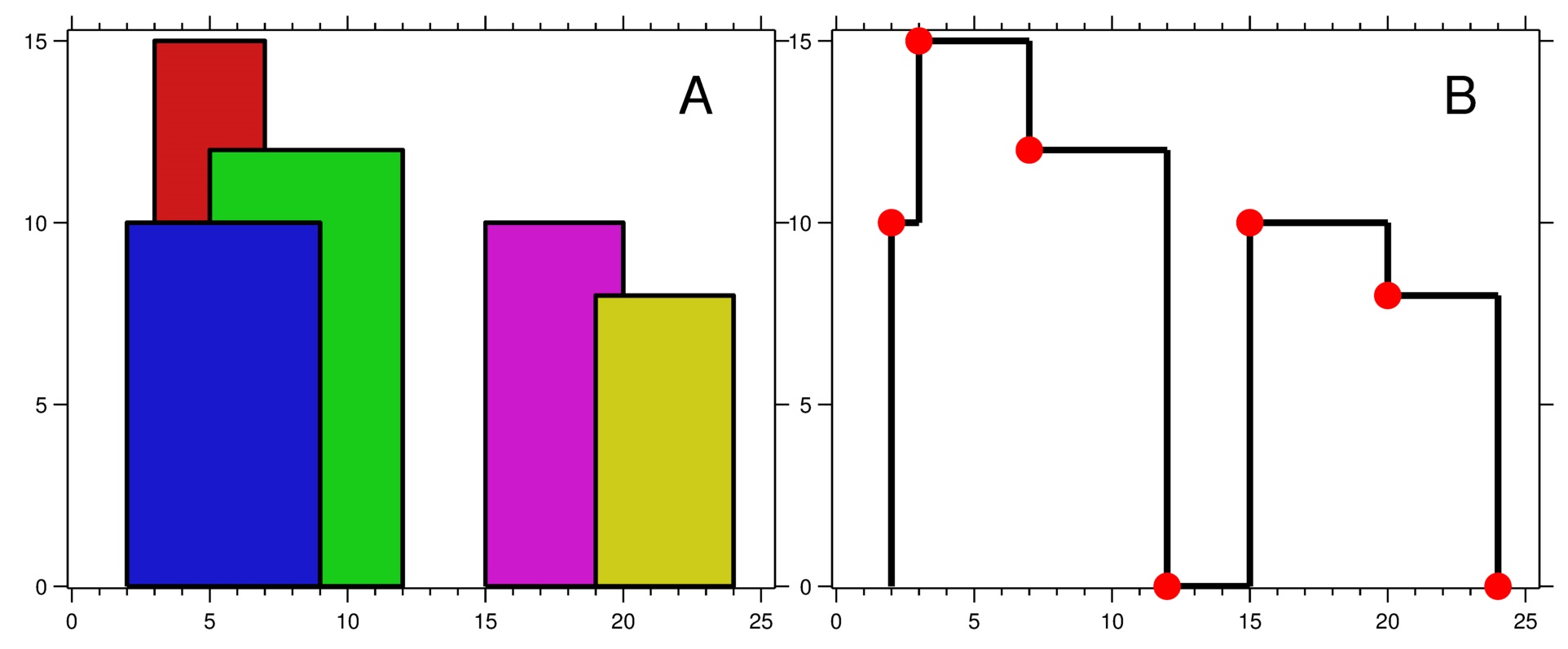
此题解采用分治和延迟传播的线段树解决天际线问题。首先,将所有建筑物的左右端点收集并去重,对这些端点进行排序和离散化,映射到连续的整数索引上。之后,使用线段树来维护每个区间的最大高度。对于每个建筑物,将其高度更新到线段树中对应的区间上。更新操作中,如果当前线段树节点的区间完全被建筑物覆盖,则使用延迟更新策略标记最大高度。最后,遍历所有的端点,查询对应的最大高度,如果与前一个高度不同,则该点是天际线的一个转折点。这样可以得到所有转折点,即城市的天际线。
时间复杂度: O(n log m)
空间复杂度: O(m)
from collections import defaultdict
class SegmentTree:
def __init__(self):
self.tree = defaultdict(lambda: 0) # 初始化线段树节点值为0
self.lazy = defaultdict(lambda: 0) # 初始化延迟更新标记为0
def pushDown(self, i):
# 延迟更新下放
if self.lazy[i]:
self.tree[2 * i] = max(self.tree[2 * i], self.lazy[i])
self.tree[2 * i + 1] = max(self.tree[2 * i + 1], self.lazy[i])
self.lazy[2 * i] = max(self.lazy[2 * i], self.lazy[i])
self.lazy[2 * i + 1] = max(self.lazy[2 * i + 1], self.lazy[i])
self.lazy[i] = 0 # 清除当前节点的延迟标记
def update(self, start, end, l, r, val, i=1):
# 区间更新操作
if l <= start and end <= r:
self.tree[i] = max(self.tree[i], val)
self.lazy[i] = max(self.lazy[i], val)
return
m = start + (end - start) // 2
self.pushDown(i) # 下放前一次的延迟更新
if l <= m:
self.update(start, m, l, r, val, 2 * i)
if r > m:
self.update(m + 1, end, l, r, val, 2 * i + 1)
self.tree[i] = max(self.tree[2 * i], self.tree[2 * i + 1]) # 更新当前节点
def query(self, start, end, l, r, i=1):
# 区间查询操作
if l <= start and end <= r:
return self.tree[i]
m = start + (end - start) // 2
self.pushDown(i) # 下放延迟更新
ans = 0
if l <= m:
ans = max(ans, self.query(start, m, l, r, 2 * i))
if r > m:
ans = max(ans, self.query(m + 1, end, l, r, 2 * i + 1))
return ans
class Solution:
def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
# 收集并离散化所有端点
xs = set()
for left, right, _ in buildings:
xs.add(left)
xs.add(right)
xs = sorted(xs) # 端点排序
n = len(xs)
dct = {x : idx for idx, x in enumerate(xs)} # 创建端点到索引的映射
# 初始化线段树并更新建筑物高度
st = SegmentTree()
for l, r, h in buildings:
st.update(0, n - 1, dct[l], dct[r] - 1, h) # 更新线段树区间
# 查询并记录天际线关键点
pre_h = 0
res = []
for x in xs:
cur_h = st.query(0, n - 1, dct[x], dct[x]) # 查询每个端点的最大高度
if cur_h != pre_h:
res.append([x, cur_h]) # 如果高度变化则记录为天际线的一个点
pre_h = cur_h
return res