用邮票贴满网格图

标签: 贪心 数组 矩阵 前缀和

难度: Hard

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

  1. 覆盖所有 空 格子。
  2. 不覆盖任何 被占据 的格子。
  3. 我们可以放入任意数目的邮票。
  4. 邮票可以相互有 重叠 部分。
  5. 邮票不允许 旋转 。
  6. 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

示例 1：

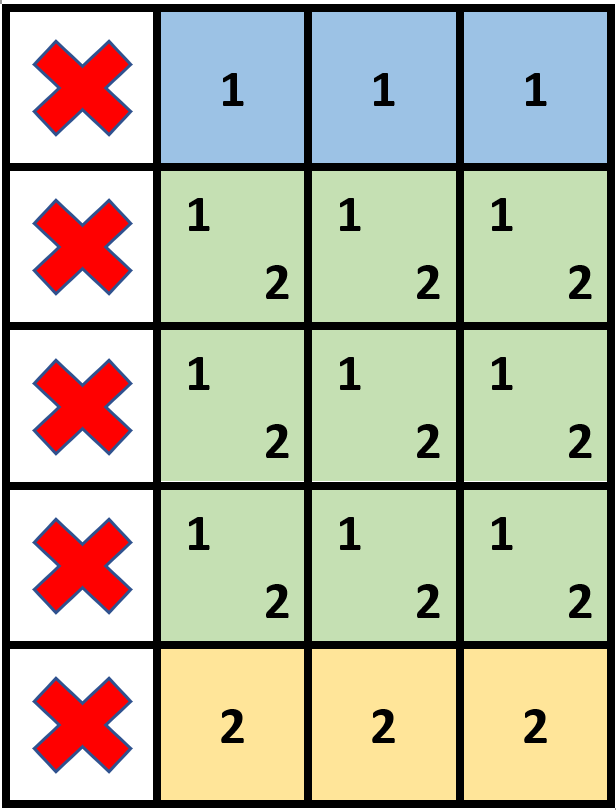
输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。

示例 2：

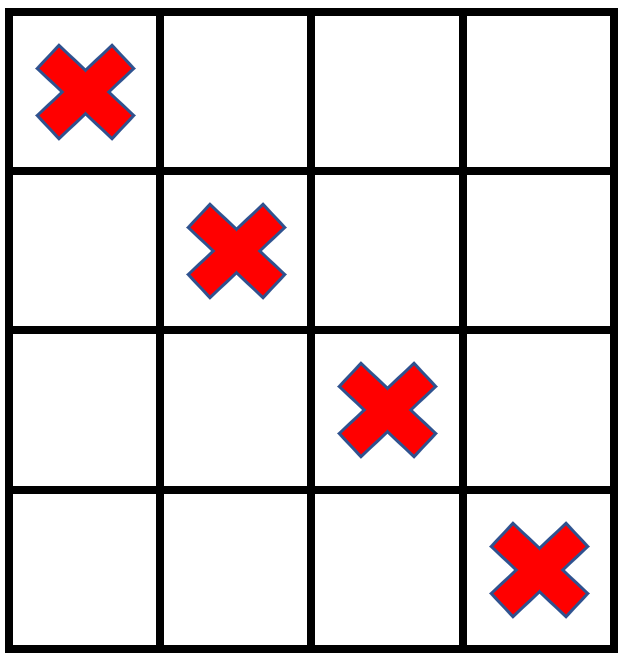
输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
输出：false 
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。

提示：

  • m == grid.length
  • n == grid[r].length
  • 1 <= m, n <= 105
  • 1 <= m * n <= 2 * 105
  • grid[r][c] 要么是 0 ，要么是 1 。
  • 1 <= stampHeight, stampWidth <= 105

Submission

运行时间: 200 ms

内存: 33.6 MB

class Solution:
    def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:
        m, n = len(grid), len(grid[0])
        psum = [[0] * (n + 2) for _ in range(m + 2)]
        diff = [[0] * (n + 2) for _ in range(m + 2)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                psum[i][j] = psum[i - 1][j] + psum[i][j - 1] - psum[i - 1][j - 1] + grid[i - 1][j - 1]

        for i in range(1, m + 2 - stampHeight):
            for j in range(1, n + 2 - stampWidth):
                x = i + stampHeight - 1
                y = j + stampWidth - 1
                if psum[x][y] - psum[x][j - 1] - psum[i - 1][y] + psum[i - 1][j - 1] == 0:
                    diff[i][j] += 1
                    diff[i][y + 1] -= 1
                    diff[x + 1][j] -= 1
                    diff[x + 1][y + 1] += 1

        for i in range(1, m + 1):
            for j in range(1, n + 1):
                diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1]
                if diff[i][j] == 0 and grid[i - 1][j - 1] == 0:
                    return False
        return True

Explain

该题解采用了差分数组和前缀和的方法来高效检查是否可以在二维网格中放置邮票。首先，构造一个前缀和矩阵 psum，用于快速计算任何子矩阵中 1 的数量。如果邮票可以放置在一个子矩阵中，那么这个子矩阵的 psum 值应为 0。接着，使用差分数组 diff 来标记可以开始放置邮票的左上角位置，并通过这个差分数组计算最终每个位置是否可以被邮票覆盖。最后遍历整个网格，如果发现有空白格子（即 grid[i][j] == 0）未被覆盖（即 diff[i][j] == 0），则返回 False，否则返回 True。

时间复杂度: O(m*n)

空间复杂度: O(m*n)

class Solution:
    def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:
        m, n = len(grid), len(grid[0])
        # 创建前缀和矩阵和差分矩阵，尺寸稍大于原网格以便处理边界条件
        psum = [[0] * (n + 2) for _ in range(m + 2)]
        diff = [[0] * (n + 2) for _ in range(m + 2)]
        # 计算网格的前缀和
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                psum[i][j] = psum[i - 1][j] + psum[i][j - 1] - psum[i - 1][j - 1] + grid[i - 1][j - 1]
        # 遍历所有可能的邮票放置起点
        for i in range(1, m + 2 - stampHeight):
            for j in range(1, n + 2 - stampWidth):
                x = i + stampHeight - 1
                y = j + stampWidth - 1
                if psum[x][y] - psum[x][j - 1] - psum[i - 1][y] + psum[i - 1][j - 1] == 0:
                    diff[i][j] += 1
                    diff[i][y + 1] -= 1
                    diff[x + 1][j] -= 1
                    diff[x + 1][y + 1] += 1
        # 应用差分数组更新覆盖情况
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1]
                if diff[i][j] == 0 and grid[i - 1][j - 1] == 0:
                    return False
        return True

Explore

在构建前缀和矩阵时，我们使用一个二维数组 `psum`，其中 `psum[i][j]` 表示从原矩阵左上角到位置 `(i-1, j-1)` 的子矩阵中所有元素的和。计算方式为 `psum[i][j] = psum[i-1][j] + psum[i][j-1] - psum[i-1][j-1] + grid[i-1][j-1]`。这种方法通过累加当前行和列的前缀和，并减去重叠部分的前缀和，再加上当前单元格的值，确保了计算的准确性。这样，任何子矩阵的元素和都可以通过四个角的 `psum` 值快速计算出来，保证了计算的准确性。

在确定邮票的起始放置点时，需要确保邮票完全位于矩阵内部。为此，我们在循环遍历潜在的起始点时，应该考虑邮票的尺寸。遍历的范围是从 `(1, 1)` 到 `(m + 1 - stampHeight, n + 1 - stampWidth)`。这样设置是因为如果起始点从这些位置开始，邮票的右下角 `(x, y)`（计算为 `x = i + stampHeight - 1`, `y = j + stampWidth - 1`）仍然保持在矩阵的边界内。这保证了每次放置邮票时，不会超过网格的边界，从而满足题目的要求。

差分数组 `diff` 用于标记可以放置邮票的左上角位置，并通过差分的方式有效地更新矩阵中的覆盖状态。当确定一个邮票可以放置在 `(i, j)` 时，我们在 `diff` 矩阵中的对应位置 `(i, j)` 增加 1，表示从这个点开始增加覆盖。同时，在 `diff[i][y+1]` 和 `diff[x+1][j]` 减去 1，表示覆盖到此结束，并在 `diff[x+1][y+1]` 加上 1，调整重叠部分的计数。这种差分的方法使得在后续通过累加得到实际的覆盖情况时，能够确保每个 `grid[i-1][j-1] == 0` 的空格子都至少被覆盖一次，如果 `diff[i][j]` 经过累加后仍为 0，则表示该空格子未被覆盖，从而可以判定邮票放置的有效性。