保证图可完全遍历

标签: 并查集 图

难度: Hard

Alice 和 Bob 共有一个无向图，其中包含 n 个节点和 3  种类型的边：

  • 类型 1：只能由 Alice 遍历。
  • 类型 2：只能由 Bob 遍历。
  • 类型 3：Alice 和 Bob 都可以遍历。

给你一个数组 edges ，其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下，找出可以删除的最大边数。如果从任何节点开始，Alice 和 Bob 都可以到达所有其他节点，则认为图是可以完全遍历的。

返回可以删除的最大边数，如果 Alice 和 Bob 无法完全遍历图，则返回 -1 。

示例 1：

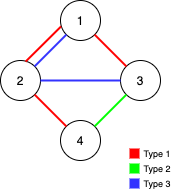
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出：2
解释：如果删除 [1,1,2] 和 [1,1,3] 这两条边，Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。

示例 2：

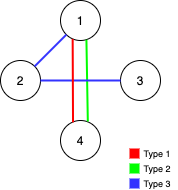
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出：0
解释：注意，删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。

示例 3：

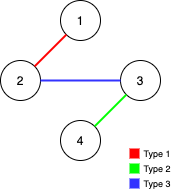
输入：n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出：-1
解释：在当前图中，Alice 无法从其他节点到达节点 4 。类似地，Bob 也不能达到节点 1 。因此，图无法完全遍历。

提示：

  • 1 <= n <= 10^5
  • 1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
  • edges[i].length == 3
  • 1 <= edges[i][0] <= 3
  • 1 <= edges[i][1] < edges[i][2] <= n
  • 所有元组 (typei, ui, vi) 互不相同

Submission

运行时间: 238 ms

内存: 52.7 MB

class UnionFind:
    def __init__(self,size):
        self.father = [None] * (size+1)
        self.num_of_sets = size
    
    def find(self,x):
        if self.father[x] is None: return x
        self.father[x] = self.find(self.father[x])
        return self.father[x]
    
    def is_connected(self,x,y):
        return self.find(x) == self.find(y)
    
    def merge(self,x,y):
        self.father[self.find(x)] = self.find(y)
        self.num_of_sets -= 1

class Solution:
    def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
        res = 0
        uf_alice = UnionFind(n)
        uf_bob = UnionFind(n)
        for _type,n1,n2 in edges:
            if _type == 3:
                if not uf_alice.is_connected(n1,n2):
                    uf_alice.merge(n1,n2)
                    uf_bob.merge(n1,n2)
                else:
                    res += 1
        for _type,n1,n2 in edges:
            if _type == 1:
                if not uf_alice.is_connected(n1,n2):
                    uf_alice.merge(n1,n2)
                else:
                    res += 1
            if _type == 2:
                if not uf_bob.is_connected(n1,n2):
                    uf_bob.merge(n1,n2)
                else:
                    res += 1

        return -1 if uf_alice.num_of_sets * uf_bob.num_of_sets > 1 else res

Explain

这道题目利用并查集来解决。首先为Alice和Bob各创建一个并查集来跟踪他们各自能够访问的节点。处理类型3的边（Alice和Bob都可以使用的边）时，首先尝试合并两个节点，如果已经在同一个集合中则认为这条边是多余的，可以删除。然后独立处理类型1和类型2的边，对于Alice和Bob的并查集分别进行操作。如果操作后两个并查集都只剩下一个集合，说明图可以被完全遍历；否则返回-1表示无法遍历。

时间复杂度: O(E)

空间复杂度: O(N)

class UnionFind:
    def __init__(self, size):
        self.father = [None] * (size + 1)  # 初始化并查集节点，初始状态下每个节点的父节点是None
        self.num_of_sets = size  # 初始化集合数量

    def find(self, x):
        if self.father[x] is None: return x  # 如果节点是根节点，返回该节点
        self.father[x] = self.find(self.father[x])  # 路径压缩
        return self.father[x]

    def is_connected(self, x, y):
        return self.find(x) == self.find(y)  # 检查两个节点是否连接

    def merge(self, x, y):
        self.father[self.find(x)] = self.find(y)  # 合并两个节点
        self.num_of_sets -= 1  # 减少集合数量

class Solution:
    def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
        res = 0
        uf_alice = UnionFind(n)
        uf_bob = UnionFind(n)
        for _type, n1, n2 in edges:
            if _type == 3:
                if not uf_alice.is_connected(n1, n2):
                    uf_alice.merge(n1, n2)
                    uf_bob.merge(n1, n2)
                else:
                    res += 1  # 计数可以删除的边
        for _type, n1, n2 in edges:
            if _type == 1:
                if not uf_alice.is_connected(n1, n2):
                    uf_alice.merge(n1, n2)
                else:
                    res += 1  # Alice并查集中多余的边
            if _type == 2:
                if not uf_bob.is_connected(n1, n2):
                    uf_bob.merge(n1, n2)
                else:
                    res += 1  # Bob并查集中多余的边

        return -1 if uf_alice.num_of_sets * uf_bob.num_of_sets > 1 else res  # 检查是否每个并查集只剩一个集合

Explore

在并查集的实现中，将每个节点的父节点初始化为None而不是其自身是为了区分根节点和未初始化的节点。这种做法允许在并查集操作中（如find和merge）更容易地管理和识别节点是否已经被访问过或加入到其他集合中。一旦节点进行了find操作或被合并到另一个节点，它的父节点将会被设置为指向它的根节点或另一个节点，这样就可以用None来表示一个节点是一个独立的根节点，即它自己就是一个集合的全部。

类型3的边是Alice和Bob都可以使用的边。当处理这类边时，即使这条边已经在Alice的并查集中存在，也需要确认它在Bob的并查集中也被合并，这样才能确保这条边对两个人的图遍历都产生作用。如果只在一个并查集中合并，而在另一个并查集中忽略，将可能导致某个人无法通过这条边连接到某些节点，从而无法完全遍历整个图。

即使在并查集中认为某些类型1或类型2的边是多余的（因为它们连接的两个节点已经在同一个集合中），仍然需要尝试进行合并操作，因为这可以确保算法的正确性和完整性。在实际操作中，这种多余的边的检测（通过检查两节点是否已连接）是在尝试合并之前进行的，这有助于在整个算法执行过程中维护并查集的当前状态，确保所有的边都被考虑过，即使它们不会改变并查集的结构。

可以通过检查每个并查集（Alice和Bob的）中的集合数量来确定是否可以完全遍历图。如果Alice的并查集只剩下一个集合，并且Bob的并查集也只剩下一个集合，这意味着所有节点都在各自的并查集中互相连接，因此可以完全遍历整个图。如果任一并查集中的集合数量大于1，则表示存在至少一个节点无法通过给定的边与其他节点连接，因此无法完全遍历图。这种方法确保了只有在两个并查集都完整连接的情况下，才认为图可以被完全遍历。