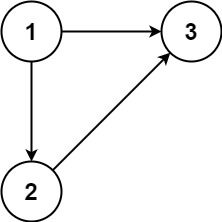
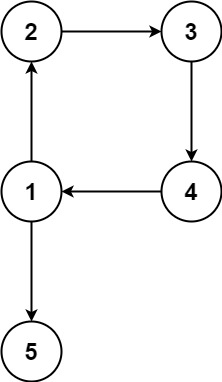
该题解使用并查集来解决问题。首先预处理边的入度数组,记录每个节点被指向的次数。然后按照特定顺序尝试删除边,判断删除后的图是否会形成环。如果删除构成入度为2的边不会形成环,说明这条边是导致冗余的边;如果删除构成入度为1的边不会形成环,说明这条边是导致冗余的边。在并查集中,如果合并两个节点时发现它们已经在同一个集合内,说明形成了环。
时间复杂度: O(n)
空间复杂度: O(n)
class UnionFindSet:
def __init__(self, n):
self.father = {}
for i in range(n):
self.father[i] = i
def add(self, x):
if x not in self.father:
self.father[x] = x
def find(self, x):
# 查找x的根节点
root = x
while self.father[root] != root:
root = self.father[root]
# 路径压缩
while self.father[x] != root:
original_father = self.father[x]
self.father[x] = root
x = original_father
return root
def union(self, x, y):
# 合并x和y所在的集合
root_x = self.find(x)
root_y = self.find(y)
if root_x == root_y:
# 若x和y已经在同一集合,返回False
return False
self.father[root_y] = root_x
return True
class Solution:
def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
length = len(edges)
# 步骤 1:预处理入度数组(记录指向某个结点的边的条数)
inDegree = [0] * (length + 1)
for edge in edges:
inDegree[edge[1]] += 1
# 步骤 2:先尝试删除构成入度为 2 的边,看看是否形成环
for i in range(length-1, -1, -1):
if inDegree[edges[i][1]] == 2:
# 如果不构成环,这条边就是要去掉的那条边
if not self.judgeCircle(edges, length, i):
return edges[i]
# 步骤 3:再尝试删除构成入度为 1 的边,看看是否形成环
for i in range(length-1, -1, -1):
if inDegree[edges[i][1]] == 1:
if not self.judgeCircle(edges, length, i):
return edges[i]
# removeEdgeIndex 删除的边的下标
# 构成环,返回 true
def judgeCircle(self, edges: List[List[int]], length: int, removeEdgeIdge) -> bool:
# 初始化并查集
ufs = UnionFindSet(length + 1)
for i in range(length):
if i == removeEdgeIdge:
# 跳过要删除的边
continue
if not ufs.union(edges[i][0], edges[i][1]):
# 合并失败,说明形成环,返回True
return True
# 无环,返回False
return False