矩阵中和能被 K 整除的路径

难度: Hard

给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发，每一步只能往下或者往右，你想要到达终点 (m - 1, n - 1) 。

请你返回路径和能被 k 整除的路径数目，由于答案可能很大，返回答案对 10⁹ + 7 取余的结果。

示例 1：

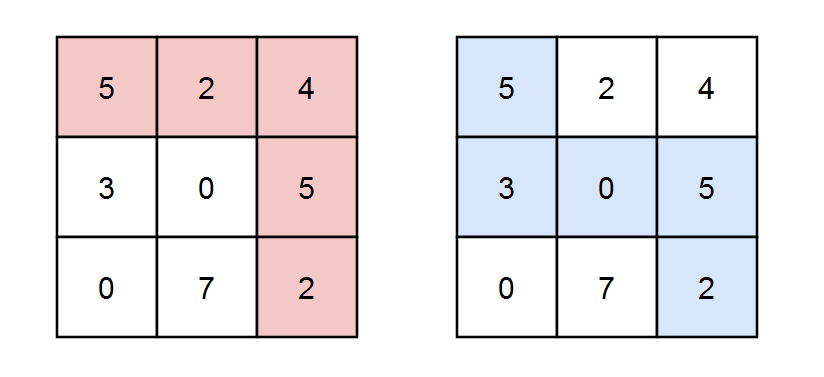
输入：grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
输出：2
解释：有两条路径满足路径上元素的和能被 k 整除。
第一条路径为上图中用红色标注的路径，和为 5 + 2 + 4 + 5 + 2 = 18 ，能被 3 整除。
第二条路径为上图中用蓝色标注的路径，和为 5 + 3 + 0 + 5 + 2 = 15 ，能被 3 整除。

示例 2：

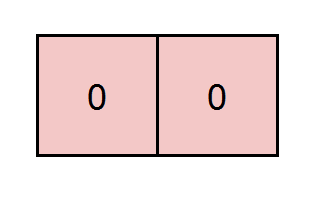
输入：grid = [[0,0]], k = 5
输出：1
解释：红色标注的路径和为 0 + 0 = 0 ，能被 5 整除。

示例 3：

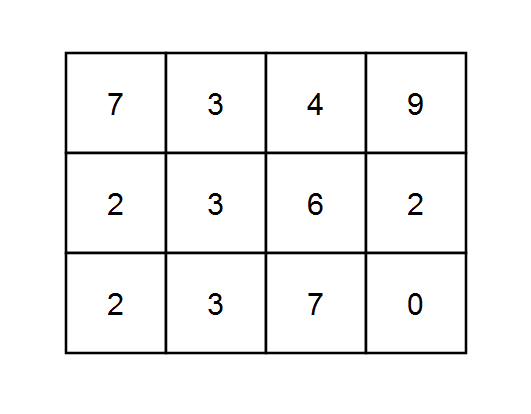
输入：grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
输出：10
解释：每个数字都能被 1 整除，所以每一条路径的和都能被 k 整除。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 5 * 10⁴
1 <= m * n <= 5 * 10⁴
0 <= grid[i][j] <= 100
1 <= k <= 50

Submission

运行时间: 863 ms

内存: 37.9 MB

class Solution:
    def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
        MOD = 10 ** 9 + 7
        m, n = len(grid), len(grid[0])
        dp = [[0] * k for _ in range(n)]
        prev = 0
        for j in range(n):
            prev = (prev + grid[0][j]) % k
            dp[j][prev] = 1
        
        prev = grid[0][0] % k
        for i in range(1, m):
            dp[0][prev] -= 1
            prev = (prev + grid[i][0]) % k
            dp[0][prev] += 1
            for j in range(1, n):
                tmp = [0] * k
                for p in range(k):
                    tmp[(grid[i][j] + p) % k] = (tmp[(grid[i][j] + p) % k] + dp[j-1][p] + dp[j][p]) % MOD
                dp[j] = tmp
        return dp[-1][0]

Explain

本题解使用动态规划的方法来解决。首先定义一个二维的 dp 数组，其中 dp[j][p] 表示到达第一行第 j 列时，路径和模 k 余 p 的路径数量。初始化第一行所有可能的路径和，然后基于第一行的结果逐行更新 dp 数组。对于每一行，我们先更新第一列的 dp 值，然后对于每一列，根据左边和上面的列的 dp 值计算当前列的 dp 值。更新规则是，对于每个可能的余数 p，计算包含当前单元格值后的新余数，并更新 dp 数组。最终，dp[n-1][0] 包含了到达右下角且路径和能被 k 整除的路径数。

时间复杂度: O(m * n * k)

空间复杂度: O(n * k)

class Solution:
    def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
        MOD = 10 ** 9 + 7
        m, n = len(grid), len(grid[0])
        dp = [[0] * k for _ in range(n)]
        prev = 0
        for j in range(n):
            prev = (prev + grid[0][j]) % k
            dp[j][prev] = 1
        
        prev = grid[0][0] % k
        for i in range(1, m):
            dp[0][prev] -= 1
            prev = (prev + grid[i][0]) % k
            dp[0][prev] += 1
            for j in range(1, n):
                tmp = [0] * k
                for p in range(k):
                    tmp[(grid[i][j] + p) % k] = (tmp[(grid[i][j] + p) % k] + dp[j-1][p] + dp[j][p]) % MOD
                dp[j] = tmp
        return dp[-1][0]

Explore

在这个问题中，使用二维数组dp[j][p]的目的是为了同时跟踪两个重要的信息：列的位置j和该位置累计路径和的模k的结果p。由于路径和的模k结果对于不同的列可以不同，而且从一列到下一列的转移依赖于前一列的所有可能的模k结果，因此需要一个二维数组来存储每一列对应的所有模k的结果。使用一维数组仅能存储单一维度的信息，无法同时处理列位置和模数的复合状态，而其他数据结构如字典或列表的列表也可以实现相同的功能，但二维数组在空间和访问效率上更优，特别是在需要频繁更新和查询的情况下。

dp数组的初始化首先涉及设置第一行的所有可能的路径和。这是通过遍历第一行的元素，累加它们的值，并计算累加和模k的结果来完成的。初始化时，dp[j][prev]被设为1，其中prev是第一行前j列元素和的模k结果。这意味着对于第一行的每个位置j，我们记录了达到该位置时，路径和模k为prev的路径数量。这种初始化方式正确反映了从矩阵的左上角到第一行任一位置的所有路径的可能模k值，为接下来的dp数组更新奠定了基础。

更新规则涉及计算当前单元格值与之前的dp值的组合，来更新当前列的dp值。具体来说，对于矩阵中的每个元素grid[i][j]，我们需要考虑从左边和上面来的所有可能的路径和的模k结果。对于每个可能的模数p(表示从上或左来的路径和模k为p)，计算新的模数(new_p)为(grid[i][j] + p) % k。然后，更新dp[j][new_p]，使其包括从左边列dp[j-1][p]和从上面行dp[j][p]来的路径数。这样的更新确保考虑了通过当前单元格的所有可能路径，并正确计算了路径和的模k结果。

在这个问题中，最终的目标是找到到达矩阵右下角，且路径和能被k整除的路径数量。dp[n-1][0]中，n-1表示最后一列，索引0表示模k结果为0，即路径和能被k整除。因此，dp[n-1][0]表示所有从左上角到右下角，且路径和模k为0的路径数量，即所有路径和能被k整除的路径数量。这是为什么我们关注dp[n-1][0]的原因，因为它直接对应于问题的要求。