并行课程 III

标签: 图 拓扑排序 数组 动态规划

难度: Hard

给你一个整数 n ，表示有 n 节课，课程编号从 1 到 n 。同时给你一个二维整数数组 relations ，其中 relations[j] = [prevCoursej, nextCoursej] ，表示课程 prevCoursej 必须在课程 nextCoursej 之前 完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 time ，其中 time[i] 表示完成第 (i+1) 门课程需要花费的 月份 数。

请你根据以下规则算出完成所有课程所需要的 最少 月份数：

  • 如果一门课的所有先修课都已经完成，你可以在 任意 时间开始这门课程。
  • 你可以 同时 上 任意门课程 。

请你返回完成所有课程所需要的 最少 月份数。

注意：测试数据保证一定可以完成所有课程（也就是先修课的关系构成一个有向无环图）。

示例 1:

输入：n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出：8
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月，课程 2 花费 2 个月。
所以，最早开始课程 3 的时间是月份 3 ，完成所有课程所需时间为 3 + 5 = 8 个月。

示例 2：

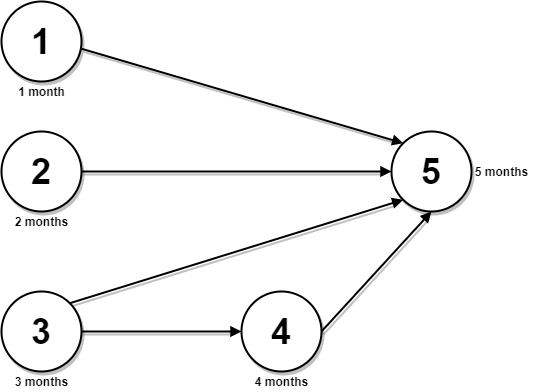
输入：n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出：12
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ，2 和 3 。
在月份 1，2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始，也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1，2，3 和 4 之后开始，也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。

提示：

  • 1 <= n <= 5 * 104
  • 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
  • relations[j].length == 2
  • 1 <= prevCoursej, nextCoursej <= n
  • prevCoursej != nextCoursej
  • 所有的先修课程对 [prevCoursej, nextCoursej] 都是 互不相同 的。
  • time.length == n
  • 1 <= time[i] <= 104
  • 先修课程图是一个有向无环图。

Submission

运行时间: 157 ms

内存: 36.5 MB

class Solution:
    def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:
        graph = [[] for _ in range(n + 1)]
        indegree = [0] * (n + 1)
        for edge in relations:
            graph[edge[0]].append(edge[1])
            indegree[edge[1]] += 1
        q = deque()
        for i in range(1, n + 1):
            if indegree[i] == 0:
                q.append(i)
        
        cost = [0] * (n + 1)
        ans = 0
        while q:
            cur =  q.popleft()
            cost[cur] += time[cur - 1]
            #ans = max(ans,cost[cur])
            ans = ans if ans > cost[cur] else cost[cur]
            for nxt in graph[cur]:
                #cost[nxt] = max(cost[nxt],cost[cur])
                cost[nxt] = cost[nxt] if cost[nxt] > cost[cur] else cost[cur]
                indegree[nxt] -= 1
                if indegree[nxt] == 0:
                    q.append(nxt)
        return ans

Explain

本题解采用拓扑排序的方法来解决有向无环图中的课程安排问题。首先，构建图的邻接表和每个节点的入度数组。使用队列来实现拓扑排序，其中队列初始包含所有入度为0的节点（即没有先修课程的课程）。在拓扑排序的过程中，我们同时计算每门课程的最早完成时间。对于每个从队列中取出的节点，更新其后继节点的最早开始时间，如果后继节点的所有前驱节点都已处理，该节点也被加入队列。最终，遍历所有课程的最早完成时间，取最大值即为完成所有课程所需的最少月份数。

时间复杂度: O(n + E)

空间复杂度: O(n + E)

class Solution:
    def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:
        graph = [[] for _ in range(n + 1)]  # 邻接表
        indegree = [0] * (n + 1)  # 入度数组
        for edge in relations:
            graph[edge[0]].append(edge[1])
            indegree[edge[1]] += 1
        q = deque()
        for i in range(1, n + 1):
            if indegree[i] == 0:
                q.append(i)  # 把没有先修课的课程加入队列
        cost = [0] * (n + 1)  # 存储每门课程的最早完成时间
        ans = 0
        while q:
            cur = q.popleft()
            cost[cur] += time[cur - 1]  # 更新当前课程的完成时间
            ans = max(ans, cost[cur])  # 记录完成所有课程的最大时间
            for nxt in graph[cur]:
                cost[nxt] = max(cost[nxt], cost[cur])  # 更新后继课程的最早开始时间
                indegree[nxt] -= 1
                if indegree[nxt] == 0:
                    q.append(nxt)  # 如果后继课程没有未完成的先修课，则加入队列
        return ans

Explore

在拓扑排序的实现中，每个节点只在其所有前驱节点都已被处理后才会被加入到队列中。节点的入度表示有多少前驱节点尚未处理。一旦节点的入度变为0，表示它的所有前驱节点已经处理完毕，它就被加入队列。从队列中取出节点时意味着这个节点正在被处理，并且每个节点都只会从队列中被取出一次，这保证了每个节点只被处理一次。

使用入度数组来帮助实现拓扑排序可以直观且有效地跟踪每个节点的前驱节点处理情况。入度数组中的每个元素记录了对应节点尚未被处理的前驱节点数量。这种方法的优势在于，可以快速检查哪些节点的所有前驱节点都已处理完毕（入度为0），这些节点就是可以加入队列并进行处理的节点。这样的处理机制简化了管理节点处理顺序的复杂度，使算法更加高效和易于实现。

使用队列（先进先出）来存储入度为0的节点，这意味着算法会按照节点达到入度为0的顺序来处理节点。这种处理方式通常保持了节点在原有图结构中的层次关系。相比之下，如果使用栈（后进先出），则可能会导致处理顺序与节点达到入度为0的顺序相反，这可以导致不同的拓扑排序结果。对于此题中计算课程的最早完成时间，使用队列确保了当一个节点被处理时，它依赖的所有课程已尽可能地早完成，有助于正确计算完成时间。使用栈则可能改变课程的处理顺序，影响对完成时间的计算。

如果有两个或多个节点同时入度为0，算法通常会按照它们被发现并加入队列的顺序来处理。在大多数实现中，这通常是按照节点编号的顺序。对于最终的课程完成月份，这种处理顺序可能会影响到某些节点的最早完成时间，特别是在节点间存在较多层级依赖时。然而，拓扑排序确保了每个节点在其所有先决条件完成后才会被处理，因此算法仍能正确计算出所有课程完成所需的最少月份数。