到达目的地的方案数

难度: Medium

你在一个城市里，城市由 n 个路口组成，路口编号为 0 到 n - 1 ，某些路口之间有双向道路。输入保证你可以从任意路口出发到达其他任意路口，且任意两个路口之间最多有一条路。

给你一个整数 n 和二维整数数组 roads ，其中 roads[i] = [u_i, v_i, time_i] 表示在路口 u_i 和 v_i 之间有一条需要花费 time_i 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。

请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大，将结果对 10⁹ + 7 取余后返回。

示例 1：

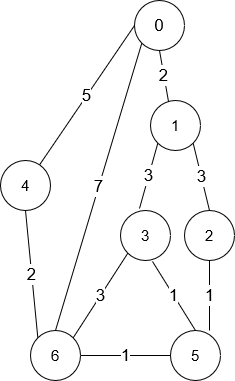
输入：n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
输出：4
解释：从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为：
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

示例 2：

输入：n = 2, roads = [[1,0,10]]
输出：1
解释：只有一条从路口 0 到路口 1 的路，花费 10 分钟。

提示：

1 <= n <= 200
n - 1 <= roads.length <= n * (n - 1) / 2
roads[i].length == 3
0 <= u_i, v_i <= n - 1
1 <= time_i <= 10⁹
u_i!= v_i
任意两个路口之间至多有一条路。
从任意路口出发，你能够到达其他任意路口。

Submission

运行时间: 40 ms

内存: 23.8 MB

from heapq import heappush, heappop
from math import inf


class Node:

    def __init__(self, w, v):
        self.w = w
        self.v = v
    
    def __lt__(self, other):
        return self.w < other.w
    
    def unpack(self):
        return [self.w, self.v]



class Solution:
    def countPaths(self, n: int, roads: List[List[int]]) -> int:
        mod = 10 ** 9 + 7
        e = [[] for _ in range(n)]
        for x, y, w in roads:
            e[x].append([y, w])
            e[y].append([x, w])
        dis = [0] + [inf] * (n - 1)
        ways = [1] + [0] * (n - 1)
        q = [Node(0, 0)]
        while q:
            cw, cv = heappop(q).unpack()
            if cw <= dis[cv]:
                for v, w in e[cv]:
                    if cw + w < dis[v]:
                        dis[v] = cw + w
                        ways[v] = ways[cv]
                        heappush(q, Node(cw + w, v))
                    elif cw + w == dis[v]:
                        ways[v] = (ways[cv] + ways[v]) % mod

        return ways[-1]

Explain

此题解采用了类似Dijkstra算法的变种，目的是找出从起点到终点的最短路径及其数量。首先，建立邻接表e存储图，dis数组记录从起点到每个点的最短距离，ways数组记录达到每个点的最短路径的数量。使用优先队列（最小堆）来持续处理当前未处理的最近的节点。每次从队列中取出当前距离最小的节点，更新其相邻节点的最短距离和路径数量。更新逻辑是：如果找到更短的路径，则更新最短路径和重置路径计数；如果距离相等，则累加路径数量。最终，ways数组的最后一个元素即为从起点到终点的最短路径的数量。

时间复杂度: O((V+E) log V)

空间复杂度: O(V+E)

from heapq import heappush, heappop
from math import inf


class Node:

    def __init__(self, w, v):
        self.w = w  # weight of the node
        self.v = v  # vertex number
    
    def __lt__(self, other):
        # Determines the order in the priority queue
        return self.w < other.w
    
    def unpack(self):
        # Helper to unpack node attributes
        return [self.w, self.v]


class Solution:
    def countPaths(self, n: int, roads: List[List[int]]) -> int:
        mod = 10 ** 9 + 7  # Modulo value for the result
        e = [[] for _ in range(n)]  # Adjacency list
        for x, y, w in roads:
            e[x].append([y, w])  # Add edge x to y
            e[y].append([x, w])  # Add edge y to x (since it's undirected)
        dis = [0] + [inf] * (n - 1)  # Distance from source
        ways = [1] + [0] * (n - 1)  # Ways to reach each node
        q = [Node(0, 0)]  # Priority queue starting with the source node
        while q:
            cw, cv = heappop(q).unpack()  # Current weight and vertex
            if cw <= dis[cv]:
                for v, w in e[cv]:
                    if cw + w < dis[v]:
                        dis[v] = cw + w  # Update distance
                        ways[v] = ways[cv]  # Update paths count
                        heappush(q, Node(cw + w, v))  # Push new distance and vertex
                    elif cw + w == dis[v]:
                        ways[v] = (ways[cv] + ways[v]) % mod  # Accumulate paths count
        return ways[-1]  # Return the number of ways to the last node

Explore

`dis`数组用于记录从起点到每个节点的最短距离，初始化为无穷大（除了起点为0），这确保了任何比当前记录更短的路径都会被考虑。`ways`数组用于记录到达每个节点的最短路径的数量，其初始化方式是起点为1，其他所有节点为0，表示从起点到起点的路径只有一条，而到达其他节点的路径数未知，初始为0。这种初始化对算法的影响是确保了只有当找到到某节点的有效路径时，该节点的路径数才会更新，避免了无效路径的计数。

优先队列（最小堆）被选择是因为它能够每次从队列中快速地获取当前未处理的最小距离节点，这是Dijkstra算法的核心要求，以此保证路径的最短性。使用普通队列或栈可能导致处理顺序不严格按照节点当前距离排序，从而无法保证每次都处理当前最短的路径，这会影响算法的正确性和效率。

这个条件用于确认从优先队列中取出的节点（其代表一条到达该节点的路径）是否仍然是有效的最短路径。在算法运行过程中，同一个节点可能因为找到更短的路径而被多次加入队列。检查`cw <= dis[cv]`确保只有对应于当前已知最短路径的节点处理逻辑会执行，从而防止对过时的路径进行错误的路径数更新。

当出现等长路径时，算法通过累加路径数量`ways[v] = (ways[cv] + ways[v]) % mod`来更新。这种方法使用了模运算来避免整数溢出，保证结果在一个安全的数值范围内。可能的计算错误主要是如果忘记应用模运算，结果可能会超出整数的表示范围，导致溢出错误。