大小为 K 的不重叠线段的数目

难度: Medium

给你一维空间的 n 个点，其中第 i 个点（编号从 0 到 n-1）位于 x = i 处，请你找到恰好 k 个不重叠 线段且每个线段至少覆盖两个点的方案数。线段的两个端点必须都是 整数坐标 。这 k 个线段不需要全部覆盖全部 n 个点，且它们的端点可以重合。

请你返回 k 个不重叠线段的方案数。由于答案可能很大，请将结果对 10⁹ + 7 取余后返回。

示例 1：

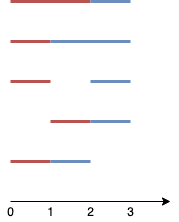
输入：n = 4, k = 2
输出：5
解释：
如图所示，两个线段分别用红色和蓝色标出。
上图展示了 5 种不同的方案 {(0,2),(2,3)}，{(0,1),(1,3)}，{(0,1),(2,3)}，{(1,2),(2,3)}，{(0,1),(1,2)} 。

示例 2：

输入：n = 3, k = 1
输出：3
解释：总共有 3 种不同的方案 {(0,1)}, {(0,2)}, {(1,2)} 。

示例 3：

输入：n = 30, k = 7
输出：796297179
解释：画 7 条线段的总方案数为 3796297200 种。将这个数对 10⁹ + 7 取余得到 796297179 。

示例 4：

输入：n = 5, k = 3
输出：7

示例 5：

输入：n = 3, k = 2
输出：1

提示：

2 <= n <= 1000
1 <= k <= n-1

Submission

运行时间: 28 ms

内存: 16.0 MB

class Solution:
    def numberOfSets(self, n: int, k: int) -> int:
        def combination(n, k, mod):
            up = 1 # 分子
            low = 1 # 分母
            for i in range(k):
                up = (up * (n - i)) % mod
                low = (low * (i + 1)) % mod
            low = pow(low, mod - 2, mod) # 费马小定理
            return up * low % mod
        mod = 10 ** 9 + 7
        return combination(n + k - 1,2 * k,mod)

Explain

该题解应用了排列组合的思路。首先，题目要求找到k个不重叠线段，每个线段至少包含两个点。因此，最少需要2k个点来形成k个线段。为了方便计算，可以将问题转化为组合问题。考虑如果把每个线段简化为两个点，那么k个线段就是选择2k个点，可以看作是从n个点中选择2k个点的组合。然而，题目中线段的端点可以重合，这意味着选取的点可以是相邻的。这种情况下，可以通过引入额外的点，将问题转化为从增广的点集中选择2k个点，点集大小为n+k-1。组合公式C(m, n)表示从m个元素中选择n个元素的组合数。题解中使用了组合公式和费马小定理来计算组合数，以避免大数的直接除法运算。

时间复杂度: O(k)

空间复杂度: O(1)

class Solution:
    def numberOfSets(self, n: int, k: int) -> int:
        def combination(n, k, mod):
            up = 1 # 分子，用于计算组合数的分子部分
            low = 1 # 分母，用于计算组合数的分母部分
            for i in range(k):
                up = (up * (n - i)) % mod # 逐一乘以每个需要的分子项，并取模
                low = (low * (i + 1)) % mod # 逐一乘以每个需要的分母项，并取模
            low = pow(low, mod - 2, mod) # 使用费马小定理计算分母的模逆
            return up * low % mod # 返回最终的组合数取模结果
        mod = 10 ** 9 + 7 # 定义模数
        return combination(n + k - 1, 2 * k, mod) # 计算并返回从增广点集中选择2k点的组合数

Explore

在题解中，`额外的点`被引入以解决线段端点可能重合的情况。这些额外的点允许我们在选择点作为线段端点时有更多的灵活性。具体来说，为了确保能够形成k个至少包含两个点的线段，我们需要在原有的n个点的基础上，考虑到端点的重合可能性，引入k-1个额外的点，使得问题转化为从`n+k-1`个点中选择`2k`个点。这些额外的点在实际问题中可以被视为虚拟的、允许重合的位置，帮助我们在逻辑上简化问题的处理。

在计算组合数的过程中，我们通常需要计算形如 `n! / (k! * (n-k)!)` 的表达式。当数值很大时，直接计算这种表达式会非常困难，因为分子和分母都可能迅速增长到超出常规计算范围。此外，在对结果需要取模的情况下，直接除法运算不适用，因为模运算的环境下除法需要被定义为乘以一个数的逆元。费马小定理提供了一种计算大数模逆的有效方法，即 `a^(p-1) ≡ 1 (mod p)` 推导出 `a^(p-2) ≡ a^(-1) (mod p)`，这样我们可以通过计算分母的模逆来有效地实现模除运算，保证计算的正确性。

题解中的方法考虑了从`n+k-1`个点中选择`2k`个点，这种方法在数学上是严格和准确的，不会发生重复计数的情况。这是因为每个组合都对应一种唯一的线段选择方式，即使是在允许线段端点重合的条件下。增加的`k-1`个点只是为了逻辑上处理端点可能的重合，实际上并不改变问题本质上的组合数计算。因此，这种方法在所有情况下都是有效且不会重复计数的。