从第一个节点出发到最后一个节点的受限路径数

标签: 图 拓扑排序 动态规划 最短路 堆（优先队列）

难度: Medium

现有一个加权无向连通图。给你一个正整数 n ，表示图中有 n 个节点，并按从 1 到 n 给节点编号；另给你一个数组 edges ，其中每个 edges[i] = [ui, vi, weighti] 表示存在一条位于节点 ui 和 vi 之间的边，这条边的权重为 weighti 。

从节点 start 出发到节点 end 的路径是一个形如 [z0, z1, z2, ..., zk] 的节点序列，满足 z0 = start 、zk = end 且在所有符合 0 <= i <= k-1 的节点 zi 和 zi+1 之间存在一条边。

路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和 x 之间路径的最短距离。受限路径 为满足 distanceToLastNode(zi) > distanceToLastNode(zi+1) 的一条路径，其中 0 <= i <= k-1 。

返回从节点 1 出发到节点 n 的 受限路径数 。由于数字可能很大，请返回对 109 + 7 取余 的结果。

 

示例 1：

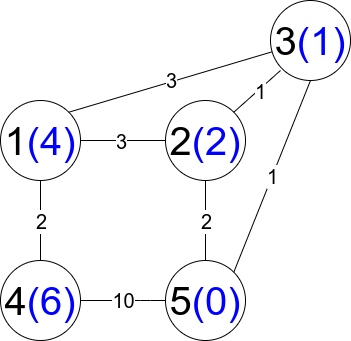
输入：n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
输出：3
解释：每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。三条受限路径分别是：
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

示例 2：

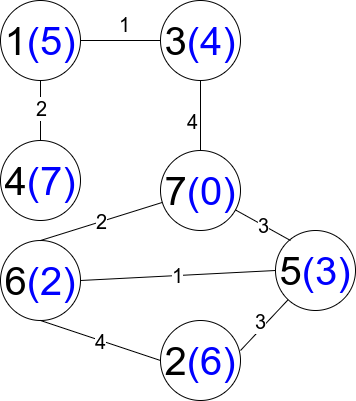
输入：n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
输出：1
解释：每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。唯一一条受限路径是：1 --> 3 --> 7 。

 

提示：

  • 1 <= n <= 2 * 104
  • n - 1 <= edges.length <= 4 * 104
  • edges[i].length == 3
  • 1 <= ui, vi <= n
  • ui != vi
  • 1 <= weighti <= 105
  • 任意两个节点之间至多存在一条边
  • 任意两个节点之间至少存在一条路径

Submission

运行时间: 286 ms

内存: 39.2 MB

class Solution:
    def countRestrictedPaths(self, n: int, edges: List[List[int]]) -> int:
        g = [[] for i in range(n)]
        for x,y,w in edges:
            g[x-1].append((y-1,w))
            g[y-1].append((x-1,w))
        dis = [inf]*(n-1)+[0]
        heap = [(0,n-1)]
        f = [0]*(n-1)+[1]
        while heap:
            dx,x = heappop(heap)
            if x==0:
                return f[0]
            if dis[x]<dx:
                continue
            for y,w in g[x]:
                new_dis = dx+w
                if dis[y]>dis[x]:
                    f[y] = (f[y]+f[x])%1000000007
                if new_dis<dis[y]:
                    dis[y] = new_dis
                    heappush(heap,(new_dis,y))

Explain

题解使用了Dijkstra算法来找出从节点n到所有其他节点的最短路径，并且用动态规划（DP）来计算受限路径的数量。首先，使用Dijkstra算法初始化最短路径数组dis，其中dis[n-1]设为0，其他节点设为无穷大，表示从n出发到该节点的最短距离。通过优先队列（堆）来保持当前的最小距离，从n开始向其他节点更新距离。对于每个节点x，检查它的所有邻接节点y，如果通过x到y的距离更短，则更新dis[y]。同时，如果dis[y] > dis[x]，说明y到x是受限路径的一部分，将从x到y的受限路径数量累加到f[y]。最后，从节点1到n的受限路径数存储在f[0]中，即最终结果。

时间复杂度: O((n + edges.length) log n)

空间复杂度: O(n + edges.length)

class Solution:
    def countRestrictedPaths(self, n: int, edges: List[List[int]]) -> int:
        g = [[] for i in range(n)]  # 初始化图的邻接表
        for x, y, w in edges:  # 构建无向图
            g[x-1].append((y-1, w))
            g[y-1].append((x-1, w))
        dis = [inf] * (n-1) + [0]  # 最短路径数组，初始化节点n的距离为0
        heap = [(0, n-1)]  # 优先队列，初始只有节点n
        f = [0] * (n-1) + [1]  # 受限路径计数数组，初始只有节点n的计数为1
        while heap:
            dx, x = heappop(heap)  # 弹出当前最小距离的节点
            if x == 0:
                return f[0]  # 如果到达节点1，返回结果
            if dis[x] < dx:
                continue  # 如果当前距离大于已知最短距离，忽略
            for y, w in g[x]:  # 遍历所有邻接节点
                new_dis = dx + w  # 更新距离
                if dis[y] > dis[x]:
                    f[y] = (f[y] + f[x]) % 1000000007  # 更新受限路径数量
                if new_dis < dis[y]:
                    dis[y] = new_dis  # 更新最短路径
                    heappush(heap, (new_dis, y))  # 将新的节点距离组合推入堆

Explore

在Dijkstra算法中，将除了起始节点（在此例中是节点n）之外的所有节点的距离初始化为无穷大，是为了确保在开始算法时，除起始节点外的其他节点都未被访问过，其最短路径未知。这种初始化方式便于在算法执行过程中，通过比较新计算的距离与已存储的距离来决定是否更新节点的最短路径。只有当通过某条路径发现更短的路径时，该节点的距离才会从无穷大更新为一个具体的值。

在Dijkstra算法的实现中，当从优先队列中取出一个节点x的距离dx，并发现dx大于该节点当前已知的最短距离dis[x]时，这通常意味着这个节点x已经被处理过，且已经找到了更短的路径到达它。这个较大的dx可能来源于之前的某个状态推入堆中的较远路径。在这种情况下，选择忽略这个较大的距离（即继续处理其他节点），而不是停止算法，是因为堆中可能还存在其他节点的更短路径需要处理。直接停止算法可能导致未处理到其他节点的最短路径。

题解中提到的判断条件基于从节点n到其他节点的最短路径的递增性来定义受限路径。理论上，如果在最短路径树中，节点y到节点x的路径满足dis[y] > dis[x]，则这条路径确实可能是一条受限路径。然而，这个条件是在最短路径已经确定的情况下判断的。如果存在多条相同长度的最短路径，或者Dijkstra算法的执行中路径更新不完全（例如由于算法提前终止或其他原因），这种情况下可能会导致误判。

动态规划数组f用于记录从节点n到每个节点的受限路径数量。数组中f[x]表示从节点n到节点x的受限路径数量。更新规则如下：当发现一条从节点x到节点y的受限路径（即dis[y] > dis[x]），则f[y]的值会加上f[x]的值，因为所有到x的受限路径现在可以扩展到y。为了防止整数溢出，还应对1000000007取模。这种方法确保了在每次找到符合受限路径条件的节点对时，从源节点到目标节点的路径数量正确地累加，从而准确计算最终的受限路径数量。