关闭分部的可行集合数目

标签: 位运算 图 枚举 最短路 堆（优先队列）

难度: Hard

一个公司在全国有 n 个分部，它们之间有的有道路连接。一开始，所有分部通过这些道路两两之间互相可以到达。

公司意识到在分部之间旅行花费了太多时间，所以它们决定关闭一些分部（也可能不关闭任何分部），同时保证剩下的分部之间两两互相可以到达且最远距离不超过 maxDistance 。

两个分部之间的 距离 是通过道路长度之和的 最小值 。

给你整数 n ，maxDistance 和下标从 0 开始的二维整数数组 roads ，其中 roads[i] = [ui, vi, wi] 表示一条从 ui 到 vi 长度为 wi的 无向 道路。

请你返回关闭分部的可行方案数目，满足每个方案里剩余分部之间的最远距离不超过 maxDistance。

注意，关闭一个分部后，与之相连的所有道路不可通行。

注意，两个分部之间可能会有多条道路。

示例 1：

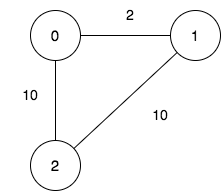
输入：n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]]
输出：5
解释：可行的关闭分部方案有：
- 关闭分部集合 [2] ，剩余分部为 [0,1] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 5 种可行的关闭方案。

示例 2：

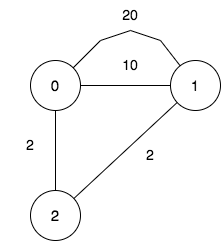
输入：n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]]
输出：7
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0,1,2] ，它们之间的最远距离为 4 。
- 关闭分部集合 [0] ，剩余分部为 [1,2] ，它们之间的距离为 2 。
- 关闭分部集合 [1] ，剩余分部为 [0,2] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 7 种可行的关闭方案。

示例 3：

输入：n = 1, maxDistance = 10, roads = []
输出：2
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0] 。
- 关闭分部集合 [0] ，关闭后没有剩余分部。
总共有 2 种可行的关闭方案。

提示：

  • 1 <= n <= 10
  • 1 <= maxDistance <= 105
  • 0 <= roads.length <= 1000
  • roads[i].length == 3
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 1 <= wi <= 1000
  • 一开始所有分部之间通过道路互相可以到达。

Submission

运行时间: 172 ms

内存: 16.8 MB

# dijkstra算法
class Solution:
    def numberOfSets(self, n: int, maxDistance: int, roads: List[List[int]]) -> int:
        road = [ defaultdict(lambda: int(1e9)) for _ in range(n) ]
        for x,y,w in roads:
            road[x][y] = min(road[x][y],w)
            road[y][x] = min(road[y][x],w)
        
        dt = [0] * (n)
        def dijkstra(start,opn):
            # dijk 最小堆优化
            heap = [(0,start)]
                    
            # 到所有点的最小距离
            dist = [int(1e9)] * n
            visit = [0] * n
            total = 0
            
            while heap:
                t,node = heappop(heap)
                
                if visit[node]:
                    continue
                
                visit[node] = 1
                total += 1
                if t > maxDistance:
                    return False
                
                for nxt,nw in road[node].items():
                    # 关闭了
                    if not dt[nxt]:
                        continue
                        
                    if dist[nxt] > t + nw:
                        dist[nxt] = t + nw
                        heappush(heap,(t+nw,nxt))
            
            # 联通点数要等于opn，即保证所有点联通
            return total == opn
                    
        # 枚举子集
        # node 当前节点
        # opn 未关闭的节点数
        def dfs(node,opn):
            if node == n:
                # 遍历所有起始点
                for start in range(n):
                    if not dt[start]:
                        continue
                    # 判断该起始点到其它点的距离符不符合要求
                    if not dijkstra(start,opn):
                        return 0
                
                return 1
                        
            
            # 选
            dt[node] = 1
            res = dfs(node+1,opn+1)
            dt[node] = 0
            
            # 不选
            res += dfs(node+1,opn)
            return res
        
        return dfs(0,0)

# # Floyd算法
# class Solution:
#     def numberOfSets(self, n: int, maxDistance: int, roads: List[List[int]]) -> int:
#         g = [[inf] * n for _ in range(n)]
#         for i in range(n):
#             g[i][i] = 0
#         for x, y, wt in roads:
#             g[x][y] = min(g[x][y], wt)
#             g[y][x] = min(g[y][x], wt)
#         print(g)
#         f = [None] * n
#         def check(s: int) -> int:
#             for i, row in enumerate(g):
#                 if s >> i & 1:
#                     f[i] = row[:]

#             # Floyd
#             for k in range(n):
#                 if (s >> k & 1) == 0: continue
#                 for i in range(n):
#                     if (s >> i & 1) == 0: continue
#                     for j in range(n):
#                         f[i][j] = min(f[i][j], f[i][k] + f[k][j])

#             for i, di in enumerate(f):
#                 if (s >> i & 1) == 0: continue
#                 for j, dij in enumerate(di):
#                     if s >> j & 1 and dij > maxDistance:
#                         return 0
#             return 1
#         return sum(check(s) for s in range(1 << n))  # 枚举子集

Explain

这个题解使用了深度优先搜索(DFS)和Dijkstra算法来找出所有可能的关闭分部的方案，满足剩余分部之间的最远距离不超过maxDistance。首先，构建了一个邻接表来表示所有分部之间的最短道路。然后，使用DFS枚举所有可能的关闭分部的子集。对于每个子集，使用Dijkstra算法检查从任一未关闭分部出发，是否所有未关闭分部都能在maxDistance的限制下互达。如果可以，这个子集是一个合法方案。

时间复杂度: O(2^n * n * E log V)

空间复杂度: O(V + E + n)

# dijkstra算法
class Solution:
    def numberOfSets(self, n: int, maxDistance: int, roads: List[List[int]]) -> int:
        # 初始化道路信息，使用邻接表存储最短距离
        road = [ defaultdict(lambda: int(1e9)) for _ in range(n) ]
        for x,y,w in roads:
            road[x][y] = min(road[x][y],w)
            road[y][x] = min(road[y][x],w)
        
        # dt数组表示分部是否关闭，0表示关闭，1表示未关闭
        dt = [0] * (n)
        # dijkstra算法实现，使用最小堆优化
        def dijkstra(start,opn):
            heap = [(0,start)]
            dist = [int(1e9)] * n
            visit = [0] * n
            total = 0
            while heap:
                t,node = heappop(heap)
                if visit[node]:
                    continue
                visit[node] = 1
                total += 1
                if t > maxDistance:
                    return False
                for nxt,nw in road[node].items():
                    if not dt[nxt]:
                        continue
                    if dist[nxt] > t + nw:
                        dist[nxt] = t + nw
                        heappush(heap,(t+nw,nxt))
            return total == opn
        # DFS遍历所有关闭分部的子集
        def dfs(node,opn):
            if node == n:
                for start in range(n):
                    if not dt[start]:
                        continue
                    if not dijkstra(start,opn):
                        return 0
                return 1
            dt[node] = 1
            res = dfs(node+1,opn+1)
            dt[node] = 0
            res += dfs(node+1,opn)
            return res
        return dfs(0,0)

Explore

在此题解中，DFS和Dijkstra算法被用于解决分部关闭问题，确保剩余分部间的最大距离不超过maxDistance。DFS（深度优先搜索）用于枚举所有可能的分部关闭子集。对每一种可能的关闭方案，DFS会遍历所有分部，决定哪些分部关闭（dt数组设为0）和哪些保持开启（dt数组设为1）。Dijkstra算法则用于验证对于每个分部关闭方案，开启的分部是否在maxDistance的限制下可以互相到达。具体地，对于每个开启的分部作为起点，使用Dijkstra算法计算其到其他所有开启分部的最短距离，并检查是否所有这些距离都不超过maxDistance。如果某一方案中所有开启的分部都是互连的，那么该方案是有效的。

在处理最短路径问题时，尤其是当图中的节点数量较大或者边的数量远少于节点对的数量时，邻接表比邻接矩阵更为高效。邻接表可以更有效地管理稀疏图，因为它只存储存在的边，而不是所有可能的节点对。这降低了内存使用，并可以减少算法在无边节点间的无效操作。在使用Dijkstra算法时，使用邻接表可以直接访问到与某个节点相连的所有节点，这使得处理动态更新距离和使用优先队列（如最小堆）检查未访问节点更为高效。

在题解中，Dijkstra算法实现确实忽略了已关闭的分部（dt[nxt]为0），不会从这些分部出发计算路径。此逻辑体现在代码中，通过`if not dt[nxt]: continue`这一行实现。这确保了算法只考虑那些保持开启的分部之间的路径。如果某一分部已经关闭，则从这一分部出发的路径不会被包括在内，因为关闭的分部不应该被计入互达性的检验中。

DFS通过递归的方式确保了每个分部都有两种可能的状态：关闭或开启。对每个分部，算法都递归地考虑了关闭它和不关闭它的情况。这种二元决策过程保证了从第一个分部到最后一个分部，所有的关闭组合都被考虑到了。具体实现中，`dfs`函数首先尝试将当前节点设为开启然后递归调用自己处理下一个分部，接着将当前节点设为关闭后再次递归调用自己。这样的递归结构保证了每一种可能的分部关闭组合都会被遍历到，从而不遗漏任何一种可能的关闭方案。