网格图中递增路径的数目

标签: 深度优先搜索 广度优先搜索 图 拓扑排序 记忆化搜索 数组 动态规划 矩阵

难度: Hard

给你一个 m x n 的整数网格图 grid ，你可以从一个格子移动到 4 个方向相邻的任意一个格子。

请你返回在网格图中从 任意 格子出发，达到 任意 格子，且路径中的数字是 严格递增 的路径数目。由于答案可能会很大，请将结果对 109 + 7 取余 后返回。

如果两条路径中访问过的格子不是完全相同的，那么它们视为两条不同的路径。

示例 1：

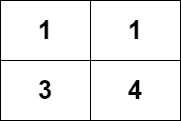
输入：grid = [[1,1],[3,4]]
输出：8
解释：严格递增路径包括：
- 长度为 1 的路径：[1]，[1]，[3]，[4] 。
- 长度为 2 的路径：[1 -> 3]，[1 -> 4]，[3 -> 4] 。
- 长度为 3 的路径：[1 -> 3 -> 4] 。
路径数目为 4 + 3 + 1 = 8 。

示例 2：

输入：grid = [[1],[2]]
输出：3
解释：严格递增路径包括：
- 长度为 1 的路径：[1]，[2] 。
- 长度为 2 的路径：[1 -> 2] 。
路径数目为 2 + 1 = 3 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 1000
  • 1 <= m * n <= 105
  • 1 <= grid[i][j] <= 105

Submission

运行时间: 642 ms

内存: 31.7 MB

class Solution:
    def countPaths(self, grid: List[List[int]]) -> int:
        MOD = 10**9 + 7
        m, n = len(grid), len(grid[0])
        # 四个方向移动的向量
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        
        # dfs函数返回从当前位置出发的递增路径数量
        def dfs(x, y):
            if not memo[x][y]:
                count = 1  # 至少包含自身
                for dx, dy in directions:
                    nx, ny = x + dx, y + dy
                    if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] > grid[x][y]:
                        count += dfs(nx, ny)
                        count %= MOD
                memo[x][y] = count
            return memo[x][y]
        
        # 初始化记忆化数组
        memo = [[0] * n for _ in range(m)]
        
        # 计算总的路径数
        total_paths = 0
        for i in range(m):
            for j in range(n):
                total_paths += dfs(i, j)
                total_paths %= MOD
        
        return total_paths

Explain

该题解采用了深度优先搜索（DFS）与记忆化的方法来解决问题。首先定义一个memo数组来存储每个格子出发的递增路径数量，避免重复计算。对于网格中的每个单元格，使用DFS探索所有可能的递增路径。通过递归调用，每次尝试向四个方向扩展路径，只有当新的单元格值大于当前单元格值时，才会继续递归搜索。每个单元格的递增路径数量是它自身（长度为1的路径）加上从它可以到达的四个方向上其他单元格的递增路径数量之和。最后，将所有单元格的路径数加起来得到总路径数。结果对1000000007取余以满足题目要求。

时间复杂度: O(m*n)

空间复杂度: O(m*n)

class Solution:
    def countPaths(self, grid: List[List[int]]) -> int:
        MOD = 10**9 + 7
        m, n = len(grid), len(grid[0])
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        
        def dfs(x, y):
            if not memo[x][y]:
                count = 1  # Start with the cell itself
                for dx, dy in directions:
                    nx, ny = x + dx, y + dy
                    if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] > grid[x][y]:
                        count += dfs(nx, ny)
                        count %= MOD
                memo[x][y] = count
            return memo[x][y]
        
        memo = [[0] * n for _ in range(m)]
        
        total_paths = 0
        for i in range(m):
            for j in range(n):
                total_paths += dfs(i, j)
                total_paths %= MOD
        
        return total_paths

Explore

在递归函数dfs中，每个单元格的初始计数设置为1是因为每个单元格本身可以视为一个长度为1的递增路径。这是路径计数的基础，确保在统计从该单元格出发的所有可能递增路径时，包括了单元格自身这一最短路径。

在进行DFS时，通过设置条件只向值更大的单元格移动来保证不会重复访问同一个单元格，因而避免形成环路。具体来说，每次递归调用只考虑那些值大于当前单元格的相邻单元格，这样的搜索路径自然不会回到已访问的单元格，因为这将意味着值减小，不符合递增路径的要求。

在每次增加路径数量后要对1000000007取余，是因为在处理大数据时，这样做可以防止整数溢出并减少计算所需的空间和时间。1000000007是一个大的质数，常用于编程竞赛和算法中作为模数，以确保结果在一个可管理的范围内。此外，MOD运算可以保证结果的一致性和安全性，特别是在可能需要网络传输或跨平台操作的情境下。

当网格尺寸非常大时，DFS的递归深度可能非常高，这可能导致算法性能下降，因为每一层递归都需要时间和空间来管理调用栈。在极端情况下，过深的递归调用可能导致栈溢出错误，尤其是在栈大小有限的系统中。为了应对这一问题，可以考虑使用迭代的深度优先搜索或广度优先搜索（BFS），或者在递归算法中引入迭代加深等技术，以控制递归深度并优化性能。