得到要求路径的最小带权子图

标签: 图 最短路

难度: Hard

给你一个整数 n ，它表示一个 带权有向 图的节点数，节点编号为 0 到 n - 1 。

同时给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi, weighti] ，表示从 fromi 到 toi 有一条边权为 weighti 的 有向 边。

最后，给你三个 互不相同 的整数 src1 ，src2 和 dest ，表示图中三个不同的点。

请你从图中选出一个 边权和最小 的子图，使得从 src1 和 src2 出发，在这个子图中，都 可以 到达 dest 。如果这样的子图不存在，请返回 -1 。

子图 中的点和边都应该属于原图的一部分。子图的边权和定义为它所包含的所有边的权值之和。

示例 1：

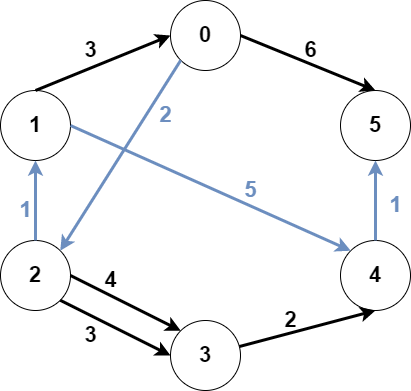
输入：n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
输出：9
解释：
上图为输入的图。
蓝色边为最优子图之一。
注意，子图 [[1,0,3],[0,5,6]] 也能得到最优解，但无法在满足所有限制的前提下，得到更优解。

示例 2：

输入：n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
输出：-1
解释：
上图为输入的图。
可以看到，不存在从节点 1 到节点 2 的路径，所以不存在任何子图满足所有限制。

提示：

  • 3 <= n <= 105
  • 0 <= edges.length <= 105
  • edges[i].length == 3
  • 0 <= fromi, toi, src1, src2, dest <= n - 1
  • fromi != toi
  • src1 ，src2 和 dest 两两不同。
  • 1 <= weight[i] <= 105

Submission

运行时间: 541 ms

内存: 80.4 MB

class Solution:
    def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:
        #s1和s2肯定是先到一个点s集合，然后到dest，枚举三段距离的和，最短的情况就是答案，注意s的方向是到dest，不能反向
        g = [[] for _ in range(n)]
        gg = [[] for _ in range(n)]
        for x, y, w in edges:
            g[x].append((y, w))
            #用于计算反向的各个节点到des的距离
            gg[y].append((x, w))

        def get_dis(s: int, dg: List) -> List[int]:
            dis = [inf] * n
            dis[s] = 0
            heap = [(0, s)]
            while heap:
                d, x = heappop(heap)
                if d > dis[x]:
                    continue
                for y, w in dg[x]:
                    dd = d + w
                    if dd < dis[y]:
                        dis[y] = dd
                        heappush(heap, (dd, y))
            return dis

        d1, d2, d3 = get_dis(src1, g), get_dis(src2, g), get_dis(dest, gg)
        ans = min(d1[i] + d2[i] + d3[i] for i in range(n))
        return ans if ans < inf else -1

Explain

为了找到一个使得从两个源点 src1 和 src2 到目的点 dest 的最小带权子图，我们需要计算从 src1 和 src2 到所有其他点的最短路径，以及从所有点到 dest 的最短路径。由于路径是有向的，计算到 dest 的最短路径需要反转边的方向，然后从 dest 出发计算到所有点的最短路径。最后，对于图中的每一个节点 i，计算 src1 到 i，src2 到 i 和 i 到 dest 的路径之和，取这些和的最小值即为所求。如果这个最小值是无穷大，说明没有这样的路径存在。

时间复杂度: O((E + V) log V)

空间复杂度: O(E + V)

class Solution:
    def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:
        from heapq import heappop, heappush
        from math import inf

        # 创建正向图和反向图
        g = [[] for _ in range(n)]
        gg = [[] for _ in range(n)]
        for x, y, w in edges:
            g[x].append((y, w))
            gg[y].append((x, w))

        # Dijkstra算法，计算单源所有点最短路径
        def get_dis(s: int, dg: List) -> List[int]:
            dis = [inf] * n
            dis[s] = 0
            heap = [(0, s)]
            while heap:
                d, x = heappop(heap)
                if d > dis[x]:
                    continue
                for y, w in dg[x]:
                    dd = d + w
                    if dd < dis[y]:
                        dis[y] = dd
                        heappush(heap, (dd, y))
            return dis

        # 计算 src1, src2 到所有点的最短路径，以及所有点到 dest 的最短路径
        d1, d2, d3 = get_dis(src1, g), get_dis(src2, g), get_dis(dest, gg)

        # 寻找满足条件的最短路径和
        ans = min(d1[i] + d2[i] + d3[i] for i in range(n))
        return ans if ans < inf else -1

Explore

Dijkstra算法是用来计算从一个源点到其他所有节点的最短路径。当需要计算从一个目标点dest到所有其他节点的最短路径时，我们无法直接应用Dijkstra算法，因为它是基于出发点而非目的点设计的。通过反转图中的所有边，每条边的方向都相反了，这样从dest出发到其他节点的路径实际上就转换成了原图中从其他节点到dest的路径。因此，反转边后使用Dijkstra算法可以有效计算从dest到所有节点的最短路径。

使用三次Dijkstra算法能够提供一种相对高效的方式来解决某些特定类型的路径问题，但这并不意味着它在所有类型的图中都是效率最优的。在稀疏图中，由于边的数量较少，Dijkstra算法（特别是使用优先队列优化的版本）通常表现良好。然而，在稠密图中，边的数量非常多，这可能会导致Dijkstra算法的运行时间增加，尤其是当图中的节点数量非常大时。在这些情况下，可能需要考虑其他算法，如Floyd-Warshall算法，该算法虽然时间复杂度高，但在处理稠密图的多源最短路径问题时可能更为适用。

通过计算得到的最短路径并不能直接保证存在一个子图使得src1和src2同时到达dest。最终算法寻找的是满足src1到i，src2到i以及i到dest的路径和最小的节点i。这意味着只有当src1和src2都可以独立到达i，且i可以到达dest时，该点i才被视为有效。如果至少存在一个这样的节点i，则可以确保存在一个子图满足题目要求。如果所有这些和都是无穷大，则不存在这样的路径，即不存在这样的子图。

代码在计算最小路径和时确实进行了必要的路径存在性验证。具体来说，通过检查每个节点i的d1[i]、d2[i]和d3[i]是否都不是无穷大，这些值表示src1到i、src2到i和i到dest的最短路径长度。只有当这三个值都有效（即不是无穷大），才会考虑这个节点i在计算最小和中。如果所有节点的三个距离之和都是无穷大，则返回-1，表示不存在满足条件的路径。因此，代码确实实现了对是否存在有效路径的检查。