多边形三角剖分的最低得分

标签: 数组 动态规划

难度: Medium

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。
 

示例 1：

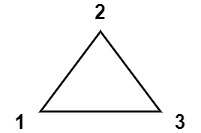
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

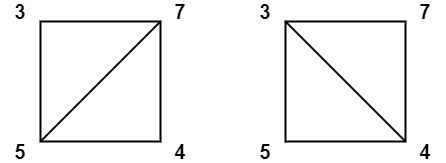
输入：values = [3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3：

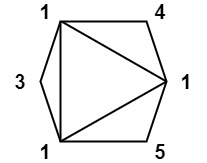
输入：values = [1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

  • n == values.length
  • 3 <= n <= 50
  • 1 <= values[i] <= 100

Submission

运行时间: 54 ms

内存: 16.0 MB

class Solution:
    def minScoreTriangulation(self, v: List[int]) -> int:
        n = len(v)
        f = [[0] * n for _ in range(n)]
        for i in range(n - 3, -1, -1):
            for j in range(i + 2, n):
                f[i][j] = min(f[i][k] + f[k][j] + v[i] * v[j] * v[k]
                              for k in range(i + 1, j))
        return f[0][-1]

Explain

这道题目是一个经典的动态规划问题，用于求多边形三角剖分的最低得分。动态规划表f[i][j]表示顶点i到顶点j的多边形剖分的最小得分。初始化f[i][j]为0，因为任何小于3个顶点的多边形不能构成三角形。动态规划的转移方程是：f[i][j] = min(f[i][k] + f[k][j] + v[i] * v[j] * v[k])，其中k从i+1到j-1。这个方程表示在顶点i到顶点j的多边形中，选择一个中间顶点k将多边形分为两部分（i到k和k到j）并加上由顶点i, j和k形成的三角形的得分。我们从小到大计算所有可能的多边形的得分，最终得到整个多边形的最小剖分得分。

时间复杂度: O(n^3)

空间复杂度: O(n^2)

class Solution:
    def minScoreTriangulation(self, v: List[int]) -> int:
        n = len(v)  # 多边形的顶点数
        f = [[0] * n for _ in range(n)]  # 动态规划表，初始化为0
        for i in range(n - 3, -1, -1):  # 从后向前遍历所有起点
            for j in range(i + 2, n):  # 遍历所有终点，至少间隔一个顶点以形成三角形
                f[i][j] = min(f[i][k] + f[k][j] + v[i] * v[j] * v[k]  # 计算剖分得分的最小值
                              for k in range(i + 1, j))  # 遍历所有可能的中间点k
        return f[0][-1]  # 返回整个多边形的最小剖分得分

Explore

选择顶点k从i+1到j-1作为中间点进行分割是为了确保每次分割都能形成至少一个有效的三角形，并且确保剩下的部分是两个较小的多边形而不是一条线段或一个点。这样的分割才能够递归地应用动态规划求解。如果k不在这个范围内，我们就不能保证每一部分至少有3个顶点，从而无法形成有效的三角形进行计算。

在动态规划中，表f[i][j]初始化为0是因为任何小于3个顶点的多边形部分不能形成三角形，因此它们的得分自然为0，不需要额外计算。动态规划的过程中，我们只计算那些至少由3个顶点组成的多边形的最小得分。因此，当j - i < 2（即两个顶点之间的距离小于2，不足以形成三角形）时，f[i][j]默认为0，这样就避免了对小于3个顶点的分割进行无效的计算。

在实际编码中，处理多边形顶点的循环通常不需要特别的数组结构，因为题目中的动态规划算法已经考虑到了顶点的循环性质。即使数组在逻辑上是循环的，我们也只需要在访问时通过取模操作来考虑这种循环性，如v[(i + k) % n]。在实现多边形剖分的动态规划时，本质上是处理一个闭环，但数组的线性表示足以覆盖所有需要的操作，因为我们只计算从i到j的闭合部分。

是的，题解中的动态规划实现通过枚举所有可能的中间顶点k从i+1到j-1，并且对每一对起点i和终点j进行计算，确保了所有可能的分割情况都被考虑到。这种方法通过从较小的多边形逐步扩展到较大的多边形，确保每一步都是基于之前计算过的最优解得出的，从而找到整个多边形剖分的最低得分。这种全面的枚举保证了最终的结果是全局最优的。