从树中删除边的最小分数

难度: Hard

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点，以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [a_i, b_i] 表示树中存在一条位于节点 a_i 和 b_i 之间的边。

删除树中两条不同的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

分别获取三个组件每个组件中所有节点值的异或值。
最大异或值和最小异或值的差值就是这一种删除边方案的分数。

例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的最小分数。

示例 1：

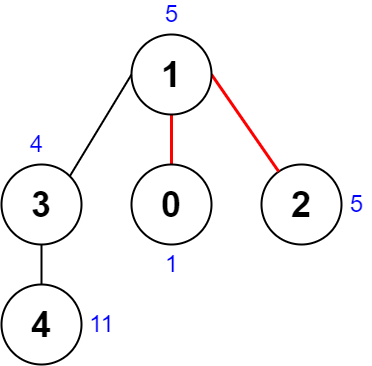
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：9
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值，10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。

示例 2：

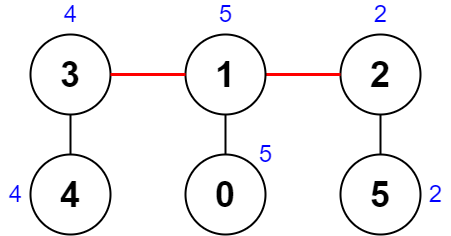
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出：0
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值，0 - 0 = 0 。
无法获得比 0 更小的分数 0 。

提示：

n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 10⁸
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges 表示一棵有效的树

Submission

运行时间: 1319 ms

内存: 17.4 MB

class Solution:
    def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
        n = len(nums)
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)
        xor, in_, out, clock = [0] * n, [0] * n, [0] * n, 0
        def dfs(x, fa):
            nonlocal clock
            clock += 1
            in_[x] = clock
            xor[x] = nums[x]
            for y in g[x]:
                if y != fa:
                    dfs(y, x)
                    xor[x] ^= xor[y]
            out[x] = clock
        dfs(0, -1)
        
        ans = inf
        for i in range(2, n):
            for j in range(1, i):
                if in_[i] < in_[j] <= out[i]:
                    x, y, z = xor[j], xor[i] ^ xor[j], xor[0] ^ xor[i]
                elif in_[j] < in_[i] <= out[j]:
                    x, y, z = xor[i], xor[i] ^ xor[j], xor[0] ^ xor[j]
                else:
                    x, y, z = xor[i], xor[j], xor[0] ^ xor[i] ^ xor[j]
                ans = min(ans, max(x, y, z) - min(x, y, z))
            if ans == 0: return 0
        return ans

Explain

该题解的核心思路是使用深度优先搜索(DFS)来计算每个子树的异或总和，并利用这些预计算的值来快速确定三个不同的连通分量的异或值。首先，构建图并通过一次DFS遍历来获得每个节点的进入和离开时间，同时计算从根节点到每个节点的异或路径值。使用这些信息，我们可以快速确定任意两条边的删除将如何分割树，并计算得到的三个分量的异或值。然后，通过尝试所有可能的边对组合来找出产生最小分数差的组合。这种方法避免了对每种可能的边对组合进行完整的DFS搜索，从而显著提高了效率。

时间复杂度: O(n^2)

空间复杂度: O(n)

class Solution:
    def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
        n = len(nums)
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)
        xor, in_, out, clock = [0] * n, [0] * n, [0] * n, 0
        def dfs(x, fa):
            nonlocal clock
            clock += 1
            in_[x] = clock
            xor[x] = nums[x]
            for y in g[x]:
                if y != fa:
                    dfs(y, x)
                    xor[x] ^= xor[y]
            out[x] = clock
        dfs(0, -1)
        
        ans = inf
        for i in range(2, n):
            for j in range(1, i):
                if in_[i] < in_[j] <= out[i]:
                    x, y, z = xor[j], xor[i] ^ xor[j], xor[0] ^ xor[i]
                elif in_[j] < in_[i] <= out[j]:
                    x, y, z = xor[i], xor[i] ^ xor[j], xor[0] ^ xor[j]
                else:
                    x, y, z = xor[i], xor[j], xor[0] ^ xor[i] ^ xor[j]
                ans = min(ans, max(x, y, z) - min(x, y, z))
            if ans == 0: return 0
        return ans

Explore

在DFS遍历中，我们通过使用一个额外的参数`fa`（表示父节点）来确保每个节点不会被重复访问。在遍历节点`x`的邻接节点`y`时，我们会检查`y`是否等于`fa`。如果不等于`fa`，则表示`y`是`x`的一个未访问过的子节点，我们可以安全地递归调用`dfs(y, x)`。这种方法可以有效地防止向父节点回溯，从而避免重复访问节点。

在DFS过程中，`in_`数组记录了每个节点的进入时间，而`out`数组记录了每个节点的离开时间。这两个时间戳可以用来判断节点的包含关系。如果节点i的进入时间和离开时间之间包含了节点j的进入时间（`in_[i] < in_[j] <= out[i]`），则节点j在节点i的子树中。这样，如果删除连接i和j的边，树将被分割成两部分：节点j的子树和包含其他所有节点的其余部分。通过这种方式，我们可以快速判断删除任意两条边后树的分割情况，进而计算分割后各部分的异或值。

异或操作具有几个特别的优势：首先，异或操作是可交换的和可结合的，这意味着元素的异或可以在任意顺序下进行，而结果不会改变。其次，异或操作满足`x ^ x = 0`和`x ^ 0 = x`的性质，这使得我们能够方便地撤销或添加节点值。在子树计算中，我们可以通过异或父节点的子树结果和当前节点值来更新异或总和。这种属性使得异或操作成为计算组合节点值的理想选择，尤其适用于需要频繁分割和合并节点值的场景，如本题的树分割问题。

在检查边的组合时，选择从`i = 2`和`j = 1`开始是为了避免重复检查边的组合并确保i和j代表不同的节点。由于在无向图中边是无序的，我们通过固定i和j的开始值和范围来避免重复计算相同的边对（例如，`[1,2]`与`[2,1]`在本题中应被视为相同）。选择这种遍历顺序是为了有效地覆盖所有需要考虑的边对组合，同时确保每个组合只被计算一次。