标签: 栈 广度优先搜索 并查集 数组 动态规划 矩阵 单调栈 堆(优先队列)
难度: Hard
给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。
当你在格子 (i, j) 的时候,你可以移动到以下格子之一:
- 满足
j < k <= grid[i][j] + j的格子(i, k)(向右移动),或者 - 满足
i < k <= grid[i][j] + i的格子(k, j)(向下移动)。
请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数,如果无法到达右下角格子,请你返回 -1 。
示例 1:
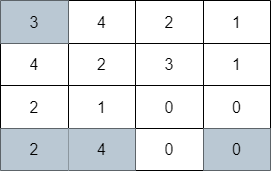
输入:grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]] 输出:4 解释:上图展示了到达右下角格子经过的 4 个格子。
示例 2:
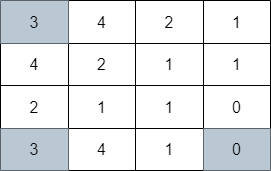
输入:grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]] 输出:3 解释:上图展示了到达右下角格子经过的 3 个格子。
示例 3:
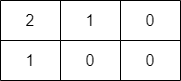
输入:grid = [[2,1,0],[1,0,0]] 输出:-1 解释:无法到达右下角格子。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 1050 <= grid[i][j] < m * ngrid[m - 1][n - 1] == 0