边权重均等查询

标签: 树 图 数组 强连通分量

难度: Hard

现有一棵由 n 个节点组成的无向树，节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。

另给你一个长度为 m 的二维整数数组 queries ，其中 queries[i] = [ai, bi] 。对于每条查询，请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中，你可以选择树上的任意一条边，并将其权重更改为任意值。

注意：

  • 查询之间 相互独立 的，这意味着每条新的查询时，树都会回到 初始状态 。
  • 从 ai 到 bi的路径是一个由 不同 节点组成的序列，从节点 ai 开始，到节点 bi 结束，且序列中相邻的两个节点在树中共享一条边。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 条查询的答案。

示例 1：

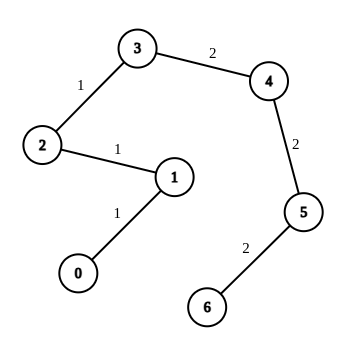
输入：n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出：[0,0,1,3]
解释：第 1 条查询，从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此，答案为 0 。
第 2 条查询，从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 0 。
第 3 条查询，将边 [2,3] 的权重变更为 2 。在这次操作之后，从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 1 。
第 4 条查询，将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后，从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

示例 2：

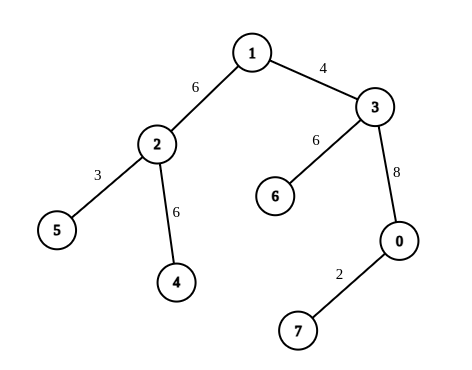
输入：n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
输出：[1,2,2,3]
解释：第 1 条查询，将边 [1,3] 的权重变更为 6 。在这次操作之后，从节点 4 到节点 6 的路径中的所有边的权重都是 6 。因此，答案为 1 。
第 2 条查询，将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后，从节点 0 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 2 。
第 3 条查询，将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后，从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此，答案为 2 。
第 4 条查询，将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后，从节点 7 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

提示：

  • 1 <= n <= 104
  • edges.length == n - 1
  • edges[i].length == 3
  • 0 <= ui, vi < n
  • 1 <= wi <= 26
  • 生成的输入满足 edges 表示一棵有效的树
  • 1 <= queries.length == m <= 2 * 104
  • queries[i].length == 2
  • 0 <= ai, bi < n

Submission

运行时间: 1250 ms

内存: 40.6 MB

class Solution:
    def minOperationsQueries(self, n: int, edges: List[List[int]], queries: List[List[int]]) -> List[int]:
        g = [{} for _ in range(n)]
        for a, b, weight in edges:
            g[a][b] = weight - 1
            g[b][a] = weight - 1
        
        root = [i for i in range(n)]
        def find(node: int) -> int:
            if root[node] != node:
                root[node] = find(root[node])
            return root[node]
        
        w = 26
        weight_cnt = [[] for i in range(n)]
        weight_cnt[0] = [0] * w
        depth = [0] * n
        
        def calc(node: int, parent: int):
            if parent != -1:
                weight_cnt[node] = weight_cnt[parent].copy()
                weight_cnt[node][g[node][parent]] += 1
            for to in g[node]:
                if to != parent:
                    depth[to] = depth[node] + 1
                    calc(to, node)
        calc(0, -1)
        
        related = [[] for _ in range(n)]
        for i, (a, b) in enumerate(queries):
            related[a].append((b, i))
            related[b].append((a, i))
        
        ans = [0 for _ in queries]
        
        visited = [False for _ in range(n)]
        def tarjan(node: int, parent: int):
            for to in g[node]:
                if to == parent:
                    continue
                tarjan(to, node)
                root[to] = node
            for other, i in related[node]:
                if visited[other]:
                    lca = find(other)
                    path_len = depth[node] + depth[other] - 2 * depth[lca]
                    cnt = [a + b - 2 * c for a, b, c in zip(weight_cnt[node], weight_cnt[other], weight_cnt[lca])]
                    ans[i] = path_len - max(cnt)
            visited[node] = True
        
        tarjan(0, -1)
        return ans

Explain

这个题解利用了图的遍历和并查集以及路径压缩的技术来找到查询中两个节点的最小公共祖先（LCA）。首先，构建了一个邻接表g来表示图，用字典存储边的权重。使用并查集来帮助找到每个节点的根节点，并在遍历过程中动态更新根节点。同时使用深度优先搜索（DFS）来计算每个节点到根节点的路径上各个权重的数量。通过比较路径上的权重来确定最小的操作次数，以使得从节点ai到bi的路径上的所有边权重相等。具体来说，对于每个查询，计算两个节点到它们的LCA的路径长度，再根据权重计数数组，找出需要改变最少的边数使得整个路径的权重一致。

时间复杂度: O((n + m) * alpha(n))

空间复杂度: O(n)

class Solution:
    def minOperationsQueries(self, n: int, edges: List[List[int]], queries: List[List[int]]) -> List[int]:
        g = [{} for _ in range(n)]
        for a, b, weight in edges:
            g[a][b] = weight - 1
            g[b][a] = weight - 1
        root = [i for i in range(n)]
        def find(node: int) -> int:
            if root[node] != node:
                root[node] = find(root[node])
            return root[node]
        w = 26
        weight_cnt = [[] for i in range(n)]
        weight_cnt[0] = [0] * w
        depth = [0] * n
        def calc(node: int, parent: int):
            if parent != -1:
                weight_cnt[node] = weight_cnt[parent].copy()
                weight_cnt[node][g[node][parent]] += 1
            for to in g[node]:
                if to != parent:
                    depth[to] = depth[node] + 1
                    calc(to, node)
        calc(0, -1)
        related = [[] for _ in range(n)]
        for i, (a, b) in enumerate(queries):
            related[a].append((b, i))
            related[b].append((a, i))
        ans = [0 for _ in queries]
        visited = [False for _ in range(n)]
        def tarjan(node: int, parent: int):
            for to in g[node]:
                if to == parent:
                    continue
                tarjan(to, node)
                root[to] = node
            for other, i in related[node]:
                if visited[other]:
                    lca = find(other)
                    path_len = depth[node] + depth[other] - 2 * depth[lca]
                    cnt = [a + b - 2 * c for a, b, c in zip(weight_cnt[node], weight_cnt[other], weight_cnt[lca])]
                    ans[i] = path_len - max(cnt)
            visited[node] = True
        tarjan(0, -1)
        return ans

Explore

在并查集中，路径压缩技术是一种优化查找操作的方法，它主要用来减少查找根节点时所需的步骤。具体操作时，当执行查找操作（find）找到根节点后，会将查找路径上的所有节点直接连接到根节点上。这样，下次再查找这些节点或其子节点时，可以直接或更快地到达根节点。在题解中，路径压缩实现如下：在递归查找函数中，当一个节点不直接指向根节点时，递归地将该节点的父节点设置为根节点，从而减少了整体的树高，提高了查找效率。

题解中提到的权重计数数组是一个二维数组，每一个元素是一个长度为26的数组（假设权重的可能值范围为0到25），用于记录从根节点到当前节点路径上每种权重出现的次数。在DFS遍历过程中，当从一个节点移动到其子节点时，会复制父节点的权重计数数组，并根据当前边的权重更新该权重的计数。具体地，如果从节点a到节点b的边权重为w，则在到达b后，权重计数数组中w索引的值会增加1。这样，每个节点的权重计数数组都能准确地反映从根节点到该节点的路径上各个权重的出现次数。

在题解中，Tarjan算法用于在线查询最小公共祖先（LCA）。它结合了DFS遍历和并查集。基本工作原理是：首先进行一次DFS遍历，遍历过程中不立即处理LCA查询。对于每个节点，首先递归处理所有子节点，每处理完一个子节点就通过并查集将其与当前节点合并，并将当前节点设置为这些子节点的新根节点。当所有子节点处理完成后，标记当前节点已访问。然后，对于与当前节点有查询关系的其他节点，如果这些节点已经被访问过，就可以立即通过并查集找到其LCA。这种方法依赖于并查集来动态维护和查询树结构，能够高效地处理和回答LCA查询。