可以到达每一个节点的最少边反转次数

标签: 深度优先搜索 广度优先搜索 图 动态规划

难度: Hard

给你一个 n 个点的 简单有向图 （没有重复边的有向图），节点编号为 0 到 n - 1 。如果这些边是双向边，那么这个图形成一棵 树 。

给你一个整数 n 和一个 二维 整数数组 edges ，其中 edges[i] = [ui, vi] 表示从节点 ui 到节点 vi 有一条 有向边 。

边反转 指的是将一条边的方向反转，也就是说一条从节点 ui 到节点 vi 的边会变为一条从节点 vi 到节点 ui 的边。

对于范围 [0, n - 1] 中的每一个节点 i ，你的任务是分别 独立 计算 最少 需要多少次 边反转 ，从节点 i 出发经过 一系列有向边 ，可以到达所有的节点。

请你返回一个长度为 n 的整数数组 answer ，其中 answer[i]表示从节点 i 出发，可以到达所有节点的 最少边反转 次数。

示例 1：

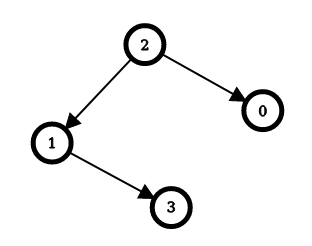
输入：n = 4, edges = [[2,0],[2,1],[1,3]]
输出：[1,1,0,2]
解释：上图表示了与输入对应的简单有向图。
对于节点 0 ：反转 [2,0] ，从节点 0 出发可以到达所有节点。
所以 answer[0] = 1 。
对于节点 1 ：反转 [2,1] ，从节点 1 出发可以到达所有节点。
所以 answer[1] = 1 。
对于节点 2 ：不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[2] = 0 。
对于节点 3 ：反转 [1,3] 和 [2,1] ，从节点 3 出发可以到达所有节点。
所以 answer[3] = 2 。

示例 2：

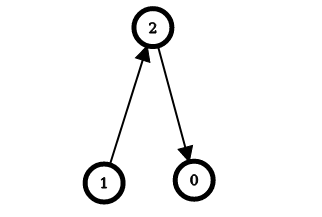
输入：n = 3, edges = [[1,2],[2,0]]
输出：[2,0,1]
解释：上图表示了与输入对应的简单有向图。
对于节点 0 ：反转 [2,0] 和 [1,2] ，从节点 0 出发可以到达所有节点。
所以 answer[0] = 2 。
对于节点 1 ：不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[1] = 0 。
对于节点 2 ：反转 [1,2] ，从节点 2 出发可以到达所有节点。
所以 answer[2] = 1 。

提示：

  • 2 <= n <= 105
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ui == edges[i][0] < n
  • 0 <= vi == edges[i][1] < n
  • ui != vi
  • 输入保证如果边是双向边，可以得到一棵树。

Submission

运行时间: 357 ms

内存: 101.0 MB

class Solution:
    def minEdgeReversals(self, n: int, edges: List[List[int]]) -> List[int]:
        nexts = [[] for _ in range(n)]
        for u, v in edges:
            nexts[u].append((v, 1))
            nexts[v].append((u, 0))
        res = [0]*n
        def dfs(i, f, depth, posAccu):
            res[i] = -depth + posAccu*2
            negs = 0
            for nex, pos in nexts[i]:
                if nex == f: continue
                negs += 1 - pos
                negs += dfs(nex, i, depth+1, posAccu+pos)
            return negs
        totalNegs = dfs(0, -1, 0, 0)
        for i in range(n):
            res[i] += totalNegs
        return res
        # down: Lu < Lv and v --> u
        # up: Lu > Lv and v --> u

Explain

这个题解采用了深度优先搜索（DFS）来解决问题。首先，构建一个图的邻接表，每个边(u, v)不仅记录目标节点v，还记录这条边的转向，如果是正向（u到v），则标记为1，反之为0。接着，从节点0开始，对图进行一次DFS遍历，计算从节点0出发到达所有节点的最少边反转次数，并记录下来。在这个过程中，计算从任意节点i到每个节点的相对深度以及到达该节点经过的正向边的数量。这些信息用于之后计算从其他节点出发到达所有节点的最少反转次数。最后，使用这些信息，通过一次循环计算出从每个节点出发的最少反转次数。

时间复杂度: O(n)

空间复杂度: O(n)

class Solution:
    def minEdgeReversals(self, n: int, edges: List[List[int]]) -> List[int]:
        nexts = [[] for _ in range(n)]  # 创建邻接表
        for u, v in edges:
            nexts[u].append((v, 1))  # 正向边
            nexts[v].append((u, 0))  # 反向边
        res = [0]*n  # 存储结果
        def dfs(i, f, depth, posAccu):
            res[i] = -depth + posAccu*2  # 计算当前节点的最少反转次数
            negs = 0  # 反向边计数
            for nex, pos in nexts[i]:
                if nex == f: continue  # 避免逆向访问父节点
                negs += 1 - pos  # 如果是反向边，增加计数
                negs += dfs(nex, i, depth+1, posAccu+pos)  # 递归处理子节点
            return negs
        totalNegs = dfs(0, -1, 0, 0)  # 从节点0开始DFS
        for i in range(n):
            res[i] += totalNegs  # 更新所有节点的结果
        return res
        # down: Lu < Lv and v --> u
        # up: Lu > Lv and v --> u

Explore

在构建邻接表时，每条边的转向标记是根据边的输入方向决定的。如果边是从节点u到节点v，那么这条边在邻接表中对于u的记录是正向（标记为1），对于v的记录则是反向（标记为0）。这种方式可以确保无论边的原始方向如何，我们都能记录从任一节点出发到另一节点的正反两个方向，从而在后续的DFS搜索中能够计算出边的反转次数。

`posAccu`参数代表从起始节点到当前节点路径上的正向边的累积数量。在DFS过程中，每遍历到一个节点，都会根据当前边是正向还是反向来更新这个累积值。这个值对计算最少边反转次数至关重要，因为它帮助我们了解到达当前节点时不需要反转的边的数量，从而能够计算出需要反转的边的总数，这直接影响到从起始点到任一节点的最少反转次数的计算。

通常在算法问题中，如果没有特别指定，节点0常被默认为起始点，这是一种常见的假设。实际上，如果图是连通的，选择不同的起始节点可能会影响到达各个节点的最少边反转次数的绝对值，但是整体的最优解的模式（即哪些边需要反转）通常是不变的。在非连通图中，起始节点的选择会更加关键，因为某些节点可能从当前起始节点根本不可达。

在DFS过程中处理环的一种常见方式是通过标记已访问的节点来避免重复访问，从而防止无限循环。对于有向图中的环，其存在确实会影响边反转的计算，因为环可能允许通过不同的路径到达同一个节点，这些路径可能需要不同数量的边反转。为了准确计算最少边反转次数，算法需要能够识别并比较通过环的不同路径所需的边反转次数。在实际实现中，可以用额外的数据结构（如`visited`数组）来跟踪访问过的节点和路径，以确保正确处理环路。