难度: Medium
给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：
0 个或是 2 个子节点。arr 中的值与树的中序遍历中每个叶节点的值一一对应。在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。
如果一个节点有 0 个子节点，那么该节点为叶节点。
示例 1：
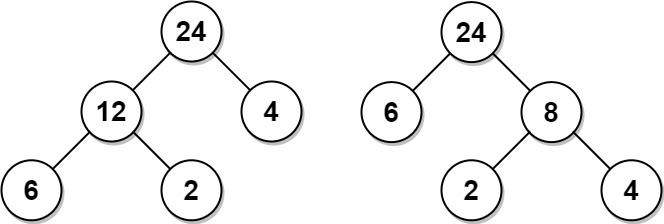
输入：arr = [6,2,4] 输出：32 解释：有两种可能的树，第一种的非叶节点的总和为 36 ，第二种非叶节点的总和为 32 。
示例 2：
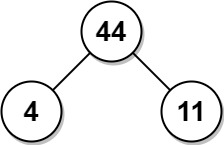
输入：arr = [4,11] 输出：44
提示：
2 <= arr.length <= 401 <= arr[i] <= 15231 。运行时间: 29 ms
内存: 16.1 MB
class Solution:
def mctFromLeafValues(self, arr: List[int]) -> int:
res = 0
stack = []
for x in arr:
if not stack:
stack.append(x)
else:
while stack and stack[-1] <= x:
y = stack.pop()
if not stack or stack[-1] > x:
res += y*x
else:
res += y*stack[-1]
stack.append(x)
while len(stack) >= 2:
x = stack.pop()
res += stack[-1] * x
return res
这个题解使用了一个单调栈的方法来寻求最小化非叶节点值的总和。核心思想是在遍历数组的过程中，通过维持一个单调递减的栈，确保每次计算的非叶节点值是局部最优的。栈中的每个元素都代表了一个潜在的叶子节点。当新的元素x大于栈顶元素时，栈顶元素将被弹出，并计算产生的非叶节点的值，这个值是弹出元素和其邻近的更大元素的乘积。这样可以保证在每个步骤中，选择的都是可能的最小的非叶节点值。最后，栈中剩余的元素将按照顺序继续计算，直到栈中仅剩一个元素。
时间复杂度: O(n)
空间复杂度: O(n)
class Solution:
def mctFromLeafValues(self, arr: List[int]) -> int:
res = 0 # 用于存储结果
stack = [] # 初始化一个空栈
for x in arr: # 遍历输入数组
if not stack: # 如果栈为空，直接添加元素
stack.append(x)
else:
while stack and stack[-1] <= x: # 维持栈的单调递减
y = stack.pop() # 弹出栈顶元素
if not stack or stack[-1] > x: # 计算非叶节点值
res += y*x
else:
res += y*stack[-1]
stack.append(x) # 将当前元素压入栈
while len(stack) >= 2: # 清空栈
x = stack.pop() # 弹出栈顶元素
res += stack[-1] * x # 计算最后的非叶节点值
return res
在单调栈解法中，当新元素x大于栈顶元素时，弹出栈顶元素并计算非叶节点值是为了维持栈的单调递减性。这种做法可以确保在每个步骤中，非叶节点的值是局部最小的。通过选择栈顶元素和其邻近的较大元素进行乘积，可以避免在之后的计算中产生更大的非叶节点值，从而在全局范围内最小化非叶节点的总和。
这种处理方式目的在于最小化新生成的非叶节点值。当弹出元素y时，如果栈不为空且栈顶元素（`stack[-1]`）大于新元素x，使用x作为乘数可以得到较小的乘积结果（因为x比栈顶元素小）。如果栈顶元素小于或等于x，则使用栈顶元素作为乘数，因为这是此时唯一可用的、相邻的较大值。这样的策略有助于在每一步保证生成的非叶节点值尽可能小，从而推动整体代价的最小化。
在处理栈中剩余的元素时，总是选择栈顶的两个元素进行计算，是因为这些元素已经是按照单调递减的顺序排列的。由于单调栈的特性，位于栈顶的两个元素是相邻的最小元素，计算它们的乘积可以保证此步骤的非叶节点值最小。考虑其他组合可能会导致更大的非叶节点值，因为这会涉及到非相邻的、可能更大的元素。
单调递减栈通过保证栈中的元素始终保持递减顺序，确保每次弹出栈顶元素时，与其相邻的元素是可能的最小值。这样在计算非叶节点值时，总是选择两个相邻最小元素的乘积，保证了每个步骤的局部最优。这种局部最优的累积最终导致了全局最优解的形成，因为每一步的最小选择减少了整体计算过程中可能出现的较大值，从而最小化了整体的非叶节点值总和。