切棍子的最小成本

难度: Hard

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

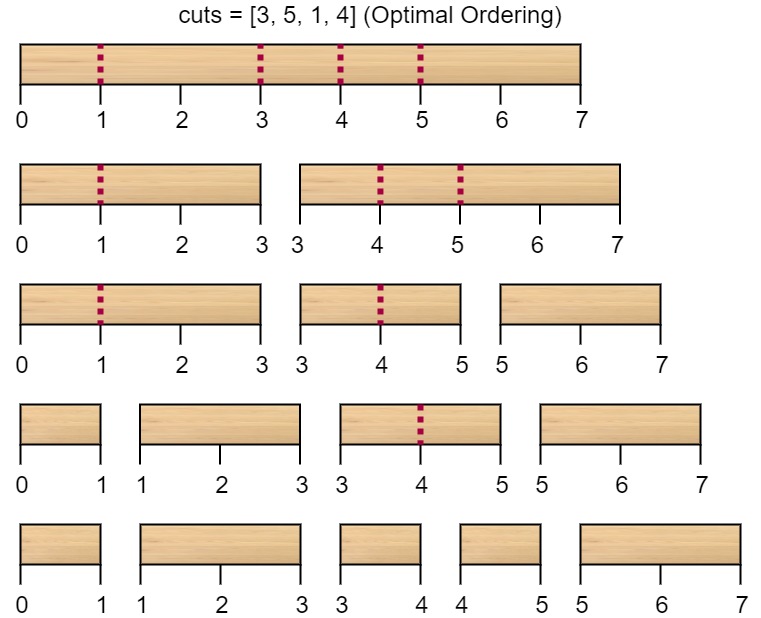
输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

提示：

2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
cuts 数组中的所有整数都 互不相同

Submission

运行时间: 234 ms

内存: 16.5 MB

class Solution:
    def minCost(self, n: int, cuts: List[int]) -> int:
        # using bottom-up method
        m = len(cuts)
        cuts = [0] + sorted(cuts) + [n]
        # cuts = sorted([0] + cuts + [n])
        dp = [[float('inf')] * (m+2) for _ in range(m+2)]

        for i in range(m+1):
            dp[i][i+1] = 0
        
        for k in range(2, m+2):
            for i in range(m -k+2):
                dp[i][i+k] = min([dp[i][j] + dp[j][i+k] for j in range(i+1, i+k)]) + cuts[i+k] - cuts[i]
        # print(dp)
        return dp[0][m+1]

Explain

这个问题可以通过动态规划来解决。首先，将切割点数组按升序排序，并在数组的起始和结尾分别添加0和n，这样方便处理边界情况。定义dp[i][j]为从切割点cuts[i]到cuts[j]的最小切割成本。初始化dp[i][i+1]为0，因为相邻切割点之间没有棍子长度，不需要成本。对于每个长度k从2到m+2，遍历所有可能的切割点对i和j，其中j=i+k。对于每对i和j，计算通过任意中间点cuts[m]切割的成本总和，选择最小的成本更新dp[i][j]。最终dp[0][m+1]将包含从0到n的整个棍子的最小切割成本。

时间复杂度: O(m^3)

空间复杂度: O(m^2)

class Solution:
    def minCost(self, n: int, cuts: List[int]) -> int:
        # 使用自底向上的动态规划方法
        m = len(cuts)
        # 在cuts数组中添加0和n，并排序
        cuts = [0] + sorted(cuts) + [n]
        # 初始化动态规划表，所有值设为无限大
        dp = [[float('inf')] * (m+2) for _ in range(m+2)]

        # 相邻切割点之间的成本为0
        for i in range(m+1):
            dp[i][i+1] = 0
        
        # 遍历所有可能的切割段长度
        for k in range(2, m+2):
            for i in range(m - k + 2):
                # 计算并更新dp[i][i+k]的最小成本
                dp[i][i+k] = min([dp[i][j] + dp[j][i+k] for j in range(i+1, i+k)]) + cuts[i+k] - cuts[i]

        # 返回整个棍子的最小切割成本
        return dp[0][m+1]

Explore

在切割点数组`cuts`中添加0和n是为了方便处理边界情况。0表示棍子的开始位置，而n表示棍子的结束位置。这样做可以确保在进行切割成本计算时，可以包括从棍子的最开始到最末端的整个区间，而无需额外的逻辑来处理这些边界条件。添加这两个点后，可以简化算法的实现，使得每个切割区间都统一处理。

在动态规划数组`dp`中，初始化值设为`float('inf')`是为了在后续的最小值比较中方便地更新成本。因为我们的目标是找到最小的切割成本，初始化为无穷大可以保证任何实际的切割成本都会小于初始化值，从而在使用`min`函数比较时，能正确地更新为较小的成本值。这是一种常见的技巧，用于确保在开始动态规划计算之前，任何未计算的值都不会影响到最终的结果。

`dp[i][i+1]`被设置为0表示相邻切割点之间没有实际的棍子长度来进行切割。因为相邻切割点代表的是同一个位置或是连续的位置，所以在这两个点之间不存在需要额外切割的部分。由于没有棍子可以被切割，因此这部分的成本自然为0。这样的设置有助于在实现算法时，为各个切割区间的成本计算提供一个正确的起始条件。

当前的方法通过枚举所有可能的中间切割点来找到使成本最小化的切割方式是一种正确的方法，但它可能不是最高效的方法。该方法的时间复杂度为O(m^3)，其中m是切割点的数量，因为它需要三层循环来计算所有可能的切割点组合。尽管这种方法是有效的，但在切割点数量非常多时可能会变得相对低效。目前动态规划是解决这类问题的标准方法，虽然有可能存在更优化的算法，比如使用更高效的数据结构或是采用不同的策略来减少计算量，但这通常需要更复杂的技术或是特定的优化技巧。