最小化旅行的价格总和

难度: Hard

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [a_i, b_i] 表示树中节点 a_i 和 b_i 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [start_i, end_i] 表示您从节点 start_i 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 end_i 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

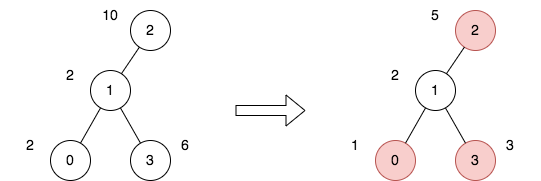
输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

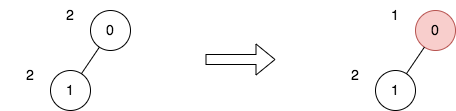
输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

1 <= n <= 50
edges.length == n - 1
0 <= a_i, b_i <= n - 1
edges 表示一棵有效的树
price.length == n
price[i] 是一个偶数
1 <= price[i] <= 1000
1 <= trips.length <= 100
0 <= start_i, end_i <= n - 1

Submission

运行时间: 53 ms

内存: 16.4 MB

class Solution:
    def minimumTotalPrice(self, n: int, edges: List[List[int]], price: List[int], trips: List[List[int]]) -> int:
        g = [[] for _ in range(n)]
        for i, j in edges:
            g[i].append(j)
            g[j].append(i)
            
        freq = [0] * n
        level = [0] * n
        parent = [0] * n
        
        def dfs(i, l, p):
            level[i] = l
            parent[i] = p
            for j in g[i]:
                if j != p:
                    dfs(j, l + 1, i)
        
        def LCA(a, b):
            if level[a] > level[b]:
                a, b = b, a
            d = level[b] - level[a]
            while d:
                b = parent[b]
                d -= 1
            if a == b:
                return a
            while a != b:
                a = parent[a]
                b = parent[b]
            return a
        
        dfs(0, 0, -1)
        for i, j in trips:
            lca = LCA(i, j)
            while i != lca:
                freq[i] += 1
                i = parent[i]
            freq[lca] += 1
            while j != lca:
                freq[j] += 1
                j = parent[j]
                
        def dp(i, p):
            res0 = 0
            res1 = price[i] // 2 * freq[i]
            for j in g[i]:
                if j != p:
                    curr = dp(j, i)
                    res0 += max(curr)
                    res1 += curr[0]
            return [res0, res1]
        
        return sum(freq[i] * price[i] for i in range(n)) - max(dp(0, -1))

Explain

该题解通过构建无向图，使用DFS确定树的层级和父子关系，并计算出所有行程中各节点被访问的频率。使用动态规划(dp)决策是否对节点价格减半以最小化旅行成本。具体步骤如下：1. 使用DFS建立树的层级结构，以便后续快速查询两节点的最近公共祖先（LCA）。2. 根据每次旅行的起止点，利用LCA和父节点信息计算出行程中的节点访问频率。3. 利用动态规划，针对每个节点决定是否减半其价格，以最小化总花费。dp函数计算两种情况：不减半和减半的总费用，并递归计算子节点的最优解。4. 最终，通过比较不减半和至少一个节点减半的总费用，得出最小的旅行总费用。

时间复杂度: O(n + t)

空间复杂度: O(n)

class Solution:
    def minimumTotalPrice(self, n: int, edges: List[List[int]], price: List[int], trips: List[List[int]]) -> int:
        g = [[] for _ in range(n)]  # 图的邻接表
        for i, j in edges:
            g[i].append(j)
            g[j].append(i)
        freq = [0] * n  # 访问频率数组
        level = [0] * n  # 节点层级
        parent = [0] * n  # 父节点数组
        def dfs(i, l, p):  # DFS定义层级和父节点
            level[i] = l
            parent[i] = p
            for j in g[i]:
                if j != p:
                    dfs(j, l + 1, i)
        def LCA(a, b):  # 计算最近公共祖先
            if level[a] > level[b]:
                a, b = b, a
            d = level[b] - level[a]
            while d:
                b = parent[b]
                d -= 1
            if a == b:
                return a
            while a != b:
                a = parent[a]
                b = parent[b]
            return a
        dfs(0, 0, -1)
        for i, j in trips:
            lca = LCA(i, j)
            while i != lca:
                freq[i] += 1
                i = parent[i]
            freq[lca] += 1
            while j != lca:
                freq[j] += 1
                j = parent[j]
        def dp(i, p):  # 动态规划决定是否减半
            res0 = 0
            res1 = price[i] // 2 * freq[i]
            for j in g[i]:
                if j != p:
                    curr = dp(j, i)
                    res0 += max(curr)
                    res1 += curr[0]
            return [res0, res1]
        return sum(freq[i] * price[i] for i in range(n)) - max(dp(0, -1))

Explore

在构建树的层级和父子关系时选择使用DFS（深度优先搜索）而不是BFS（广度优先搜索），主要是因为DFS可以在遍历过程中直接递归地设置每个节点的父节点和层级，而无需额外的数据结构来维护队列。此外，DFS可以在一次遍历中直接深入到树的最深层，然后逐层返回，递归地构建整个树结构，这在逻辑上更为直接和简洁。相比之下，BFS需要使用队列来维护当前层的所有节点，对于只是建立层级和父子关系的需求可能显得更复杂。

函数`LCA(a, b)`（最近公共祖先）能够在所有情况下正确返回两个节点的最近公共祖先，是通过保证两个节点在同一层级上相遇。具体步骤如下：首先，如果a和b在不同层级，则将更深的节点向上移动，直到两节点处于同一层级。然后，如果a和b不相同，同时将两节点向它们的父节点移动，直到它们相遇。这种方法确保了无论树的结构如何，都可以通过逐级向上追溯找到a和b的公共祖先。

`dp(i, p)`函数在动态规划部分中返回两个值，分别代表以下意义：第一个值（`res0`）代表在节点i及其子树中，如果节点i的价格不减半时，从节点i开始的所有子树的最优总花费。第二个值（`res1`）则代表在节点i及其子树中，如果节点i的价格减半时，从节点i开始的所有子树的最优总花费。这两个值通过递归计算i的所有子节点的最优解，并结合i节点本身的费用状态（减半或不减半），来决定整棵子树的最优花费策略。