本题解利用了最小生成树的 Kruskal 算法和离散化结合线段树优化的方法来寻找连接所有点的最小费用。首先,通过构建四种变换的点集,以应对曼哈顿距离的计算特点,并通过排序和离散化来优化处理。利用线段树(通过二分索引树BIT实现)维护每个离散化后位置的最小距离和对应索引,来高效地查询和更新边的最小费用。然后,将所有潜在的边加入到边列表中。最后,通过Kruskal算法,利用并查集(Disjoint Set Union, DSU)来确定最小生成树,从而找出所有点连接的最小总费用。
时间复杂度: O(n log n)
空间复杂度: O(n)
class DisjointSetUnion:
def __init__(self, n):
self.n = n # 节点数量
self.rank = [1] * n # 用于优化并查集的rank数组
self.f = list(range(n)) # 并查集的父节点数组
def find(self, x: int) -> int: # 查找根节点,并进行路径压缩
if self.f[x] == x:
return x
self.f[x] = self.find(self.f[x])
return self.f[x]
def unionSet(self, x: int, y: int) -> bool: # 合并两个节点
fx, fy = self.find(x), self.find(y)
if fx == fy:
return False
if self.rank[fx] < self.rank[fy]:
fx, fy = fy, fx
self.rank[fx] += self.rank[fy]
self.f[fy] = fx
return True
class BIT:
def __init__(self, n):
self.n = n # 节点数加1,用于线段树操作
self.tree = [float("inf")] * n # 线段树存储最小值
self.idRec = [-1] * n # 记录最小值对应的节点索引
self.lowbit = lambda x: x & (-x) # 计算最低有效位
def update(self, pos: int, val: int, identity: int): # 更新线段树
while pos > 0:
if self.tree[pos] > val:
self.tree[pos] = val
self.idRec[pos] = identity
pos -= self.lowbit(pos)
def query(self, pos: int) -> int: # 查询给定范围内的最小值和索引
minval, j = float("inf"), -1
while pos < self.n:
if minval > self.tree[pos]:
minval = self.tree[pos]
j = self.idRec[pos]
pos += self.lowbit(pos)
return j
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int: # 主函数
n = len(points) # 点的数量
edges = list() # 存储所有边的列表
def build(pos: List[Tuple[int, int, int]]): # 构建边的函数
pos.sort() # 对点进行排序
a = [y - x for (x, y, _) in pos] # 计算曼哈顿距离的一部分
b = sorted(set(a)) # 离散化处理
num = len(b) # 离散化后的数量
bit = BIT(num + 1) # 创建线段树
for i in range(n - 1, -1, -1): # 逆序处理以维护正确的最小值
poss = bisect.bisect(b, a[i]) # 二分查找离散化位置
j = bit.query(poss) # 查询最小值对应的索引
if j != -1: # 如果找到有效的最小值
dis = abs(pos[i][0] - pos[j][0]) + abs(pos[i][1] - pos[j][1]) # 计算曼哈顿距离
edges.append((dis, pos[i][2], pos[j][2])) # 将边加入到列表中
bit.update(poss, pos[i][0] + pos[i][1], i) # 更新线段树
def solve(): # 处理所有变换并构建边
pos = [(x, y, i) for i, (x, y) in enumerate(points)] # 原始坐标
build(pos) # 构建边
pos = [(y, x, i) for i, (x, y) in enumerate(points)] # 交换x, y以处理不同的曼哈顿距离
build(pos)
pos = [(-y, x, i) for i, (x, y) in enumerate(points)] # 反转y坐标
build(pos)
pos = [(x, -y, i) for i, (x, y) in enumerate(points)] # 反转x坐标
build(pos)
solve() # 调用solve函数构建所有边
dsu = DisjointSetUnion(n) # 创建并查集实例
edges.sort() # 根据边的权重排序,以便Kruskal算法处理
ret, num = 0, 1 # 初始化最小生成树的总权重和计数器
for length, x, y in edges: # 遍历所有边
if dsu.unionSet(x, y): # 尝试合并节点
ret += length # 累加权重
num += 1 # 增加计数器
if num == n: # 如果已经连接了所有节点
break
return ret # 返回最小生成树的总权重
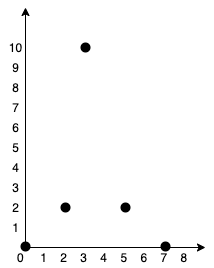
我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。 注意到任意两个点之间只有唯一一条路径互相到达。