难度: Medium
给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。
请你返回元素总和小于或等于阈值的正方形区域的最大边长；如果没有这样的正方形区域，则返回 0 。
示例 1：
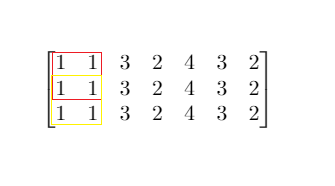
输入：mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4 输出：2 解释：总和小于或等于 4 的正方形的最大边长为 2，如图所示。
示例 2：
输入：mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1 输出：0
提示：
m == mat.lengthn == mat[i].length1 <= m, n <= 3000 <= mat[i][j] <= 1040 <= threshold <= 105 运行时间: 133 ms
内存: 22.7 MB
class Solution:
def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
r = len(mat)
c = len(mat[0])
s = [[0]*(c+1) for _ in range(r+1)]
for i in range(1,c+1):
s[1][i] = s[1][i-1] + mat[0][i-1]
for i in range(1,r+1):
for j in range(1,c+1):
s[i][j] = s[i-1][j]+s[i][j-1]+mat[i-1][j-1]-s[i-1][j-1]
ans = 0
for k in range(1,min(r,c)+1):
for i in range(r-k+1):
for j in range(c-k+1):
su = s[i+k][j+k]-s[i+k][j]-s[i][j+k]+s[i][j]
if su <= threshold:
ans = k
break
if su <= threshold:break
if ans == k-1:break
return ans
该题解采用了二维前缀和数组以及二分搜索的策略：首先，构建一个二维前缀和数组s，使得s[i][j]表示从(0,0)到(i-1,j-1)的矩阵内所有元素的和。构建这个数组后，可以快速计算任意子矩阵的和。接着，通过遍历所有可能的正方形边长k，并对矩阵中的每个起点(i,j)计算边长为k的正方形的元素和，如果和小于等于阈值，则更新最大边长。此外，如果在某一边长k下，找到了满足条件的正方形，就直接跳到下一个边长，否则提前终止循环。
时间复杂度: O(m*n*min(m,n))
空间复杂度: O(m*n)
class Solution:
def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
r = len(mat) # 矩阵的行数
c = len(mat[0]) # 矩阵的列数
s = [[0]*(c+1) for _ in range(r+1)] # 构建前缀和数组，大小为 (r+1) x (c+1)
# 初始化第一行的前缀和
for i in range(1, c+1):
s[1][i] = s[1][i-1] + mat[0][i-1]
# 构造完整的前缀和矩阵
for i in range(1, r+1):
for j in range(1, c+1):
s[i][j] = s[i-1][j] + s[i][j-1] + mat[i-1][j-1] - s[i-1][j-1]
ans = 0 # 最大边长初始化为0
# 尝试每一个可能的正方形边长k
for k in range(1, min(r, c) + 1):
found = False # 标记是否找到满足条件的正方形
for i in range(r - k + 1):
for j in range(c - k + 1):
su = s[i+k][j+k] - s[i+k][j] - s[i][j+k] + s[i][j] # 计算边长为k的正方形的元素和
if su <= threshold:
ans = k # 更新最大边长
found = True # 标记找到满足条件的正方形
break
if found: break
if not found: break # 如果这个边长没有找到满足条件的正方形，结束循环
return ans # 返回最大边长
在构建二维前缀和数组时，选择使用(r+1) x (c+1)的大小是为了处理边界条件，便于计算包含矩阵边界的子矩阵的元素和。如果使用r x c大小，那么在计算位于矩阵顶部或左侧边界的子矩阵时，会需要额外的条件判断来避免索引越界。通过引入额外的一行和一列（初始化为0），可以使任意子矩阵的元素和的计算公式保持一致，简化编程实现。
这个公式是基于二维前缀和数组的性质推导出来的。s[i][j]表示从(0,0)到(i-1,j-1)的矩阵内所有元素的和。要计算从(i,j)起始、边长为k的正方形的元素和，需要从s[i+k][j+k]（包含整个大矩阵的和）中减去上方的矩形和s[i+k][j]和左侧的矩形和s[i][j+k]，然后加上因为重复减去的左上角小矩阵s[i][j]。这样就得到了仅包括目标正方形内的元素和。
这种做法不会错过更大边长满足条件的正方形。因为如果边长为k的正方形的元素和已经超过阈值，那么边长大于k的正方形（包含更多的元素）更有可能超过阈值。反之，如果找到了满足条件的边长k，那么尝试更大的边长是合理的，因为这可能找到更大的满足条件的正方形。
这是基于问题的性质和优化效率的考虑。如果在尝试某一特定边长k时未找到任何满足条件的正方形，意味着所有的k x k的正方形的元素和都超过了阈值。因此，对于任何大于k的边长，其构成的正方形只会包含更多的元素，其和也更有可能超过阈值。继续增加边长并尝试会导致不必要的计算，因此在找不到满足条件的正方形时提前终止循环是一种有效的优化策略。