在树上执行操作以后得到的最大分数

难度: Medium

有一棵 n 个节点的无向树，节点编号为 0 到 n - 1 ，根节点编号为 0 。给你一个长度为 n - 1 的二维整数数组 edges 表示这棵树，其中 edges[i] = [a_i, b_i] 表示树中节点 a_i 和 b_i 有一条边。

同时给你一个长度为 n 下标从 0 开始的整数数组 values ，其中 values[i] 表示第 i 个节点的值。

一开始你的分数为 0 ，每次操作中，你将执行：

选择节点 i 。
将 values[i] 加入你的分数。
将 values[i] 变为 0 。

如果从根节点出发，到任意叶子节点经过的路径上的节点值之和都不等于 0 ，那么我们称这棵树是 健康的 。

你可以对这棵树执行任意次操作，但要求执行完所有操作以后树是 健康的 ，请你返回你可以获得的 最大分数 。

示例 1：

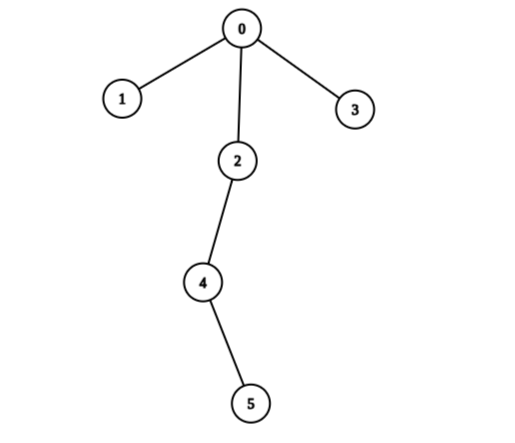
输入：edges = [[0,1],[0,2],[0,3],[2,4],[4,5]], values = [5,2,5,2,1,1]
输出：11
解释：我们可以选择节点 1 ，2 ，3 ，4 和 5 。根节点的值是非 0 的。所以从根出发到任意叶子节点路径上节点值之和都不为 0 。所以树是健康的。你的得分之和为 values[1] + values[2] + values[3] + values[4] + values[5] = 11 。
11 是你对树执行任意次操作以后可以获得的最大得分之和。

示例 2：

输入：edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [20,10,9,7,4,3,5]
输出：40
解释：我们选择节点 0 ，2 ，3 和 4 。
- 从 0 到 4 的节点值之和为 10 。
- 从 0 到 3 的节点值之和为 10 。
- 从 0 到 5 的节点值之和为 3 。
- 从 0 到 6 的节点值之和为 5 。
所以树是健康的。你的得分之和为 values[0] + values[2] + values[3] + values[4] = 40 。
40 是你对树执行任意次操作以后可以获得的最大得分之和。

提示：

2 <= n <= 2 * 10⁴
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
values.length == n
1 <= values[i] <= 10⁹
输入保证 edges 构成一棵合法的树。

Submission

运行时间: 156 ms

内存: 31.8 MB

class Solution:
    # # 树形 DP：选或不选
    # 正难则反
    # https://leetcode.cn/problems/maximum-score-after-applying-operations-on-a-tree/solutions/2513101/shu-xing-dpxuan-huo-bu-xuan-pythonjavacg-7aj6/
    def maximumScoreAfterOperations(self, edges: List[List[int]], values: List[int]) -> int:
        g = [[] for _ in values]
        g[0].append(-1)  # 避免误把根节点当作叶子
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)

        # dfs(x, fa) 计算以 x 为根的子树是健康时，失去的最小分数
        def dfs(x: int, fa: int) -> int:
            if len(g[x]) == 1:  # x 是叶子
                return values[x]
            loss = 0  # 第二种情况
            for y in g[x]:
                if y != fa:
                    loss += dfs(y, x)  # 计算以 y 为根的子树是健康时，失去的最小分数
            return min(values[x], loss)  # 两种情况取最小值
        return sum(values) - dfs(0, -1)

Explain

此题解采用了树形动态规划的方法来解决问题。首先构建一个图表示树的结构，然后通过深度优先搜索（DFS）计算以每个节点为根的子树在保持健康的条件下能够保留的最小分数。对于每个节点，如果它是叶子节点，则其最小分数即为节点自身的值；如果不是叶子节点，则需要比较该节点值与其所有子节点通过DFS计算得到的分数之和，取较小者作为该节点的最小分数。最后，总分减去根节点的最小分数即为可以获得的最大分数。

时间复杂度: O(n)

空间复杂度: O(n)

class Solution:
    def maximumScoreAfterOperations(self, edges: List[List[int]], values: List[int]) -> int:
        # 构建邻接列表表示树的结构
        g = [[] for _ in values]
        g[0].append(-1)  # 避免根节点被误判为叶子节点
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)

        # dfs(x, fa) 计算以 x 为根的子树保持健康时的最小失分
        def dfs(x: int, fa: int) -> int:
            if len(g[x]) == 1:  # 判断 x 是否为叶子节点
                return values[x]
            loss = 0  # 计算非叶子节点的最小失分
            for y in g[x]:
                if y != fa:
                    loss += dfs(y, x)  # 递归计算子节点的最小失分
            return min(values[x], loss)  # 取节点值与子节点失分和的较小者
        # 计算总分减去根节点的最小失分得到最大可得分
        return sum(values) - dfs(0, -1)

Explore

在构建邻接列表时，给根节点添加一个-1作为父节点主要是为了在DFS过程中方便地处理根节点。这样，在执行DFS函数时，可以利用这个-1来识别并跳过根节点的父节点检查，从而避免错误地将根节点视为叶子节点。如果不加这个特殊的父节点，DFS在访问根节点时可能会误判其为叶子节点，因为它没有其他父节点信息。

在`dfs`函数中，如果一个非叶子节点的子节点总和小于该节点的值，选择子节点总和而不是节点的值作为返回结果是为了最小化该节点及其子树的总失分。目的是在整个树中尽可能保留更多的分数。如果选择节点的值而不是子节点的总和，虽然当前节点的失分更小，但可能导致整体失分增加，因为子节点的分数可能全部丢失。通过取较小者，我们保证了从整棵树的角度来看，失分是最小的。

在题解中提到的`健康的树`暗示了树结构在执行操作后仍应保持其基本结构与功能，即尽可能保留更多节点的原始值。通过DFS计算最小失分，我们实际上是在尝试通过选择每个节点与其子树可能产生的最小失分来维持树的'健康'。这种方法确保了在减少总失分的同时，保持了树结构和节点值的最优保存，从而与题目要求的保持树的健康性相吻合。

在极端情况下，如果树形结构为一条直线，那么递归调用的最大深度将等于树的节点数，也就是说，递归深度为N，其中N是树的节点总数。在这种情况下，如果N非常大，确实有可能导致栈溢出错误，因为每层递归调用都需要消耗一定的栈空间。在实际应用中，可以通过采用迭代方法或者在语言支持的情况下增加栈大小等方式来避免这种情况。