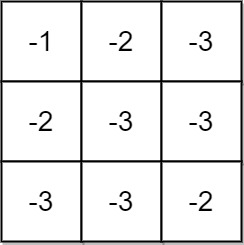
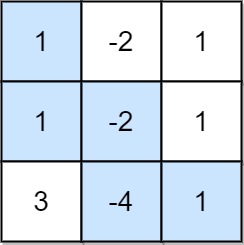
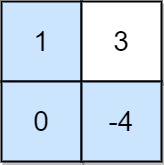
该题解采用动态规划的方法来解决问题。定义两个二维数组 max_product 和 min_product,其中 max_product[i][j] 存储到达单元格 (i, j) 的所有路径中可能的最大积,min_product[i][j] 存储可能的最小积。这是因为负数的存在,最小积乘以负数可能变成最大积。初始状态设置为 max_product[0][0] 和 min_product[0][0] 等于 grid[0][0]。然后分别初始化矩阵的第一行和第一列。对于其他单元格,根据当前单元格值的正负来决定如何更新 max_product 和 min_product。遍历完成后,max_product[m-1][n-1] 存储的就是到达右下角的最大积。如果这个最大积小于 0,直接返回 -1;否则,返回其对 10^9+7 取模的结果。
时间复杂度: O(m*n)
空间复杂度: O(m*n)
class Solution:
def maxProductPath(self, grid: List[List[int]]) -> int:
MOD = 10 ** 9 + 7
m, n = len(grid), len(grid[0])
# 初始化最大积和最小积矩阵
max_product = [[0] * n for _ in range(m)]
min_product = [[0] * n for _ in range(m)]
# 填充第一行和第一列
max_product[0][0] = min_product[0][0] = grid[0][0]
for i in range(1, m):
max_product[i][0] = max_product[i-1][0] * grid[i][0]
min_product[i][0] = min_product[i-1][0] * grid[i][0]
for j in range(1, n):
max_product[0][j] = max_product[0][j-1] * grid[0][j]
min_product[0][j] = min_product[0][j-1] * grid[0][j]
# 填充其他格子
for i in range(1, m):
for j in range(1, n):
if grid[i][j] >= 0:
max_product[i][j] = max(max_product[i-1][j], max_product[i][j-1]) * grid[i][j]
min_product[i][j] = min(min_product[i-1][j], min_product[i][j-1]) * grid[i][j]
else:
max_product[i][j] = min(min_product[i-1][j], min_product[i][j-1]) * grid[i][j]
min_product[i][j] = max(max_product[i-1][j], max_product[i][j-1]) * grid[i][j]
# 检查最大非负积是否为负数
if max_product[-1][-1] < 0:
return -1
# 取余并返回结果
return max_product[-1][-1] % MOD