堆叠长方体的最大高度

标签: 数组 动态规划 排序

难度: Hard

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti]（下标从 0 开始）。请你从 cuboids 选出一个 子集 ，并将它们堆叠起来。

如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。

返回 堆叠长方体 cuboids 可以得到的 最大高度 。

 

示例 1：

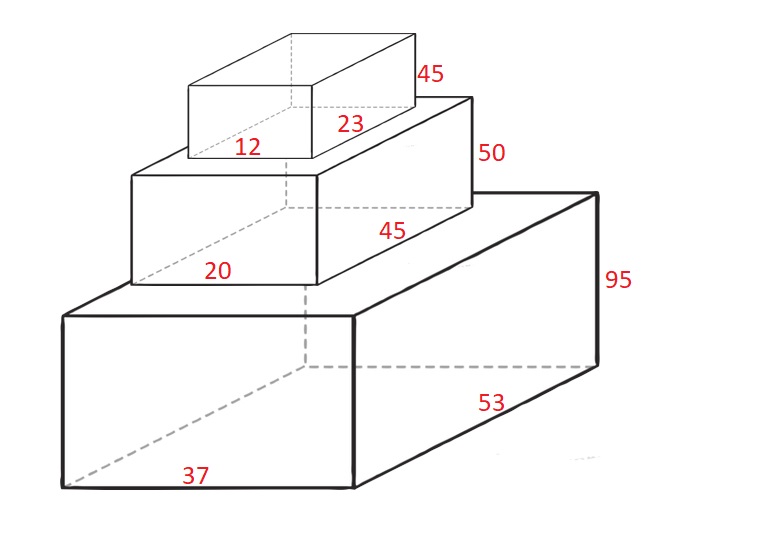
输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

示例 2：

输入：cuboids = [[38,25,45],[76,35,3]]
输出：76
解释：
无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

示例 3：

输入：cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
输出：102
解释：
重新排列长方体后，可以看到所有长方体的尺寸都相同。
你可以把 11x7 的一面朝下，这样它们的高度就是 17 。
堆叠长方体的最大高度为 6 * 17 = 102 。

 

提示：

  • n == cuboids.length
  • 1 <= n <= 100
  • 1 <= widthi, lengthi, heighti <= 100

Submission

运行时间: 31 ms

内存: 16.1 MB

class Solution:
    def maxHeight(self, cuboids: List[List[int]]) -> int:
        for c in cuboids:  # 宽长高递增排序
            c.sort()
        cuboids.sort()  # 盒子排序

        f = [0] * len(cuboids)

        for i, (_, l2, h2) in enumerate(cuboids):
            for j, (_, l1, h1) in enumerate(cuboids[:i]):
                if l1 <= l2 and h1 <= h2:  # 排序后，w1 <= w2 恒成立
                    f[i] = max(f[i], f[j])  # cuboids[j] 可以堆在 cuboids[i] 上
            f[i] += h2

        return max(f)

Explain

这个问题可以通过动态规划解决。首先，我们需要处理每个长方体，让它的三个维度按照非降序排序，这样对于每个长方体，我们总是可以确保宽度是最小的，长度是中等的，高度是最大的。接着，我们对整个长方体数组进行排序，这样我们可以基于宽度和长度的非降序来处理它们。在动态规划数组 `f` 中，`f[i]` 表示以第 `i` 个长方体为顶部的最大堆叠高度。对于每个长方体 `i`，我们会遍历在它之前的所有长方体 `j`，检查是否可以将 `j` 堆叠在 `i` 上。这是基于比较长度和高度，因为宽度已经通过排序保证了。如果可以堆叠，我们就更新 `f[i]` 为 `f[j] + height of i` 中的最大值。最后，我们的答案是 `f` 中的最大值，即所有可能的堆叠配置中的最大高度。

时间复杂度: O(n^2)

空间复杂度: O(n)

class Solution:
    def maxHeight(self, cuboids: List[List[int]]) -> int:
        for c in cuboids:  # 对每个长方体的尺寸进行排序，确保宽度<=长度<=高度
            c.sort()
        cuboids.sort()  # 对所有长方体整体排序，基于宽度和长度

        f = [0] * len(cuboids)  # 动态规划数组，f[i]表示以cuboids[i]为顶部的最大堆叠高度

        for i, (_, l2, h2) in enumerate(cuboids):  # 遍历每个长方体i
            for j, (_, l1, h1) in enumerate(cuboids[:i]):  # 检查所有在i之前的长方体j
                if l1 <= l2 and h1 <= h2:  # 如果长方体j可以放在长方体i上
                    f[i] = max(f[i], f[j] + h2)  # 更新堆叠高度
        return max(f)  # 返回最大的堆叠高度

Explore

对每个长方体的尺寸进行非降序排序（即确保宽度<=长度<=高度），是为了简化后续的堆叠长方体的逻辑。这样排序后，对于每个长方体，我们总是确保在堆叠时，可以按照固定的维度顺序（宽度、长度、高度）进行比较和堆叠。这种排序方式还保证了在比较两个长方体的堆叠可能性时，我们只需要比较长度和高度，因为宽度已经通过排序保证了适当的顺序。

在进行所有长方体的整体排序时，排序依据是首先基于宽度，然后是长度。这种排序方式确保了在动态规划过程中，遍历当前长方体 `i` 时，可以直接通过比较长度和高度来判断之前的长方体 `j` 是否可以堆叠在 `i` 上，而无需再次考虑宽度，因为宽度已经通过排序保证了非降序。这样的排序方式有助于简化堆叠条件的判断，提高算法的效率。

动态规划数组 `f[i]` 表示以第 `i` 个长方体为顶部的最大堆叠高度。在更新 `f[i]` 时，`f[i] = max(f[i], f[j] + h2)` 的逻辑是为了确保 `f[i]` 可以从所有可能的 `j` (即可以堆叠在 `i` 上的长方体) 中获得最大的堆叠高度。这里的 `h2` 是当前考虑的长方体 `i` 的高度。所以，`f[j] + h2` 表示如果将长方体 `i` 堆叠在长方体 `j` 上，得到的新的堆叠高度。通过这种方式，我们可以保证每个 `f[i]` 都是基于前面所有可能的堆叠配置的最大高度。