T 秒后青蛙的位置

难度: Hard

给你一棵由 n 个顶点组成的无向树，顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下：

在一秒内，青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点（如果它们直接相连）。
青蛙无法跳回已经访问过的顶点。
如果青蛙可以跳到多个不同顶点，那么它跳到其中任意一个顶点上的机率都相同。
如果青蛙不能跳到任何未访问过的顶点上，那么它每次跳跃都会停留在原地。

无向树的边用数组 edges 描述，其中 edges[i] = [a_i, b_i] 意味着存在一条直接连通 a_i 和 b_i 两个顶点的边。

返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10^-5 的结果将被视为正确答案。

示例 1：

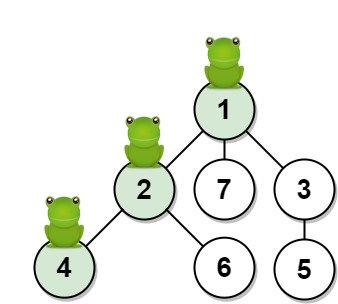
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出：0.16666666666666666 
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，第 1 秒 有 1/3 的概率跳到顶点 2 ，然后第 2 秒 有 1/2 的概率跳到顶点 4，因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。

示例 2：

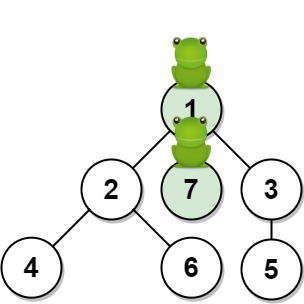
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出：0.3333333333333333
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。

提示：

1 <= n <= 100
edges.length == n - 1
edges[i].length == 2
1 <= a_i, b_i <= n
1 <= t <= 50
1 <= target <= n

Submission

运行时间: 25 ms

内存: 16.3 MB

class Solution:
    def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:
        g = [[] for _ in range(n + 1)]
        g[1] = [0]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)
        
        ans = 0

        def dfs(x: int, fa: int, left_t: int, prod: int) -> bool:
            if x == target and (left_t == 0 or len(g[x]) == 1):
                nonlocal ans
                ans = 1 / prod
                return True
            if x == target or left_t == 0:
                return False
            for y in g[x]:
                if y != fa and dfs(y, x, left_t - 1, prod * (len(g[x]) - 1)):
                    return True
            return False
        
        dfs(1, 0, t, 1)
        return ans

Explain

这个题解使用了深度优先搜索（DFS）来解决问题。首先，将无向树的边转换成邻接表表示，确保从任意节点都可以访问到其相邻节点。特殊地，节点1做了初始化处理，以0作为一个标记节点。在DFS过程中，算法尝试从节点1开始探索，每次递归探索其邻居节点，同时更新剩余时间（left_t）和到达当前节点的概率乘积（prod）。当到达目标节点时，如果剩余时间为0或该节点没有其他可以跳转的邻居节点，那么这就是一条有效的路径，其路径概率就是要求的答案。若在时间耗尽之前到达目标节点，或者无法继续向下搜索，则终止当前路径的探索。

时间复杂度: O(n * t)

空间复杂度: O(n)

class Solution:
    def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:
        g = [[] for _ in range(n + 1)]  # 创建邻接表
        g[1] = [0]  # 初始化节点1
        for x, y in edges:  # 构建无向图的邻接表
            g[x].append(y)
            g[y].append(x)
        
        ans = 0  # 最终结果的存储变量

        def dfs(x: int, fa: int, left_t: int, prod: int) -> bool:
            if x == target and (left_t == 0 or len(g[x]) == 1):  # 到达目标且满足结束条件
                nonlocal ans
                ans = 1 / prod  # 计算概率
                return True
            if x == target or left_t == 0:  # 达到目标或时间用尽，结束搜索
                return False
            for y in g[x]:  # 遍历所有邻居节点
                if y != fa and dfs(y, x, left_t - 1, prod * (len(g[x]) - 1)):  # 递归探索
                    return True
            return False
        
        dfs(1, 0, t, 1)  # 从节点1开始DFS
        return ans  # 返回结果

Explore

在这个问题中，`prod`参数代表的是从起点到当前节点的路径概率乘积，而不是累加和，因为概率的传递是乘法关系，不是加法。例如，如果青蛙从一个节点跳到另一个节点的概率是独立的，并且与之前的跳跃无关，那么到达当前节点的总概率是之前所有跳跃概率的乘积。累加和通常用于计算总和或平均等，而不适用于概率的连续传递。

检查`left_t == 0`或者`len(g[x]) == 1`的条件是为了确认青蛙是否停留在目标节点。`left_t == 0`意味着没有剩余时间，即青蛙必须停在当前位置；而`len(g[x]) == 1`意味着目标节点没有其他邻居可以跳转（因为唯一的邻居是来时的节点），所以青蛙也必须停留。如果这两个条件都不满足，即使青蛙到达了目标节点，它仍有可能跳到其他节点，不符合题目要求青蛙确切停在目标节点的场景。

在题解中，0用作特殊标记来表示节点1的父节点，这在DFS中是常见的技巧来防止回溯到起始节点。选择0作为标记是因为在大多数编程语言中，列表或数组的索引通常从1开始，使用0作为不存在的或虚拟的节点可以有效避免混淆，并且简化条件判断。其他数字或方法也可以使用，但使用0是因为它在程序设计中通常代表'无'或'不存在'，清晰且易于理解。

`fa`在这个上下文中代表'父节点'，即当前节点的前一个节点。在DFS遍历中，`y != fa`的判断用来确保搜索不会返回到上一个访问的节点（即不会走回头路），这是避免在无向图中造成无限循环的重要条件。通过这种方式，算法确保每个节点仅被访问一次，除非它是通过其他路径重新访问的。