人员站位的方案数 II

难度: Hard

给你一个 n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [x_i, y_i] 。

我们定义 x 轴的正方向为右（x 轴递增的方向），x 轴的负方向为左（x 轴递减的方向）。类似的，我们定义 y 轴的正方向为上（y 轴递增的方向），y 轴的负方向为下（y 轴递减的方向）。

你需要安排这 n 个人的站位，这 n 个人中包括 Alice 和 Bob 。你需要确保每个点处恰好有一个人。同时，Alice 想跟 Bob 单独玩耍，所以 Alice 会以 Alice 的坐标为 左上角 ，Bob 的坐标为 右下角 建立一个矩形的围栏（注意，围栏可能不包含任何区域，也就是说围栏可能是一条线段）。如果围栏的内部或者边缘上有任何其他人，Alice 都会难过。

请你在确保 Alice 不会难过的前提下，返回 Alice 和 Bob 可以选择的点对数目。

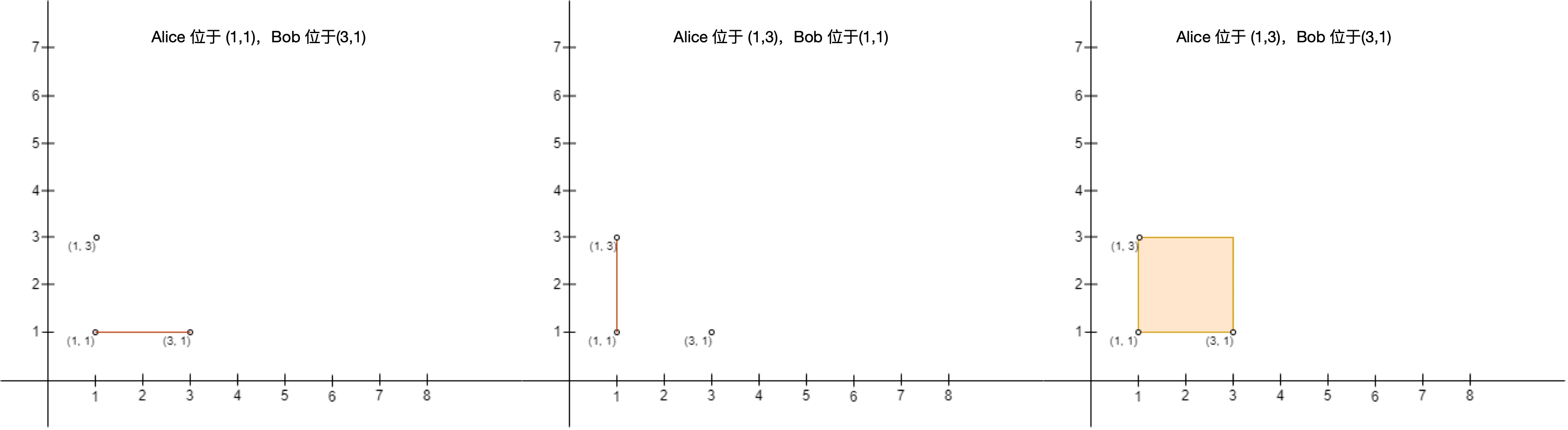
注意，Alice 建立的围栏必须确保 Alice 的位置是矩形的左上角，Bob 的位置是矩形的右下角。比方说，以 (1, 1) ，(1, 3) ，(3, 1) 和 (3, 3) 为矩形的四个角，给定下图的两个输入，Alice 都不能建立围栏，原因如下：

图一中，Alice 在 (3, 3) 且 Bob 在 (1, 1) ，Alice 的位置不是左上角且 Bob 的位置不是右下角。
图二中，Alice 在 (1, 3) 且 Bob 在 (1, 1) ，Bob 的位置不是在围栏的右下角。

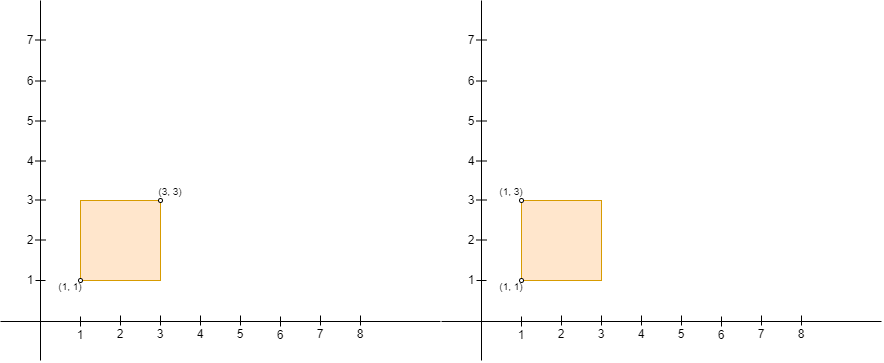
示例 1：

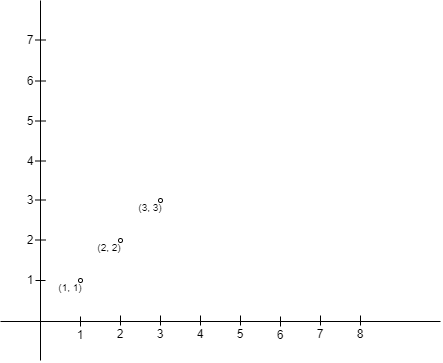
输入：points = [[1,1],[2,2],[3,3]]
输出：0
解释：没有办法可以让 Alice 的围栏以 Alice 的位置为左上角且 Bob 的位置为右下角。所以我们返回 0 。

示例 2：

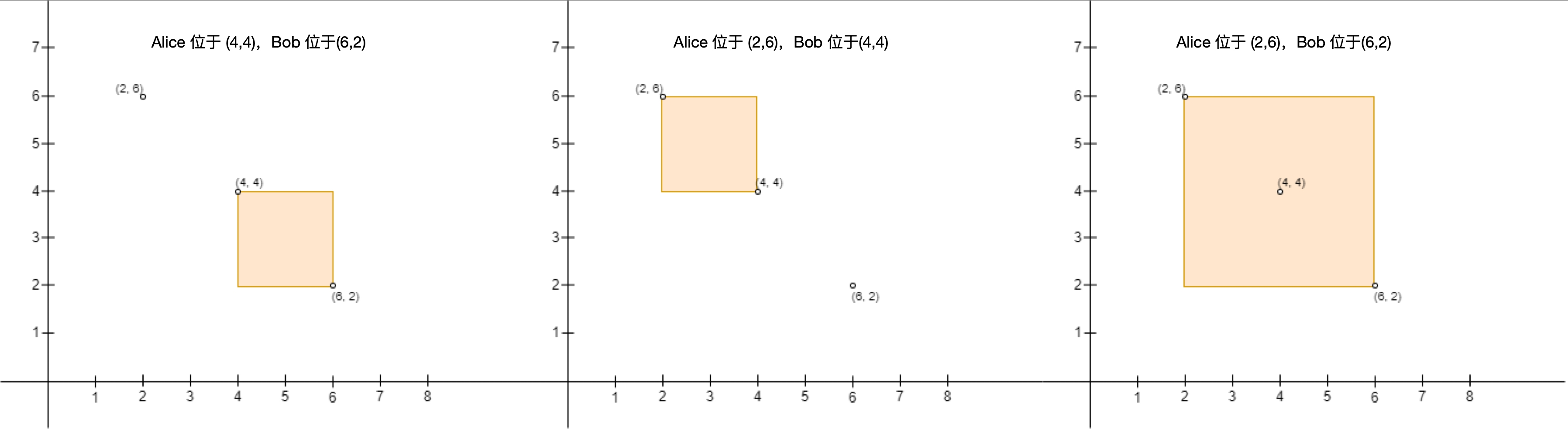
输入：points = [[6,2],[4,4],[2,6]]
输出：2
解释：总共有 2 种方案安排 Alice 和 Bob 的位置，使得 Alice 不会难过：
- Alice 站在 (4, 4) ，Bob 站在 (6, 2) 。
- Alice 站在 (2, 6) ，Bob 站在 (4, 4) 。
不能安排 Alice 站在 (2, 6) 且 Bob 站在 (6, 2) ，因为站在 (4, 4) 的人处于围栏内。

示例 3：

输入：points = [[3,1],[1,3],[1,1]]
输出：2
解释：总共有 2 种方案安排 Alice 和 Bob 的位置，使得 Alice 不会难过：
- Alice 站在 (1, 1) ，Bob 站在 (3, 1) 。
- Alice 站在 (1, 3) ，Bob 站在 (1, 1) 。
不能安排 Alice 站在 (1, 3) 且 Bob 站在 (3, 1) ，因为站在 (1, 1) 的人处于围栏内。
注意围栏是可以不包含任何面积的，上图中第一和第二个围栏都是合法的。

提示：

2 <= n <= 1000
points[i].length == 2
-10⁹ <= points[i][0], points[i][1] <= 10⁹
points[i] 点对两两不同。

Submission

运行时间: 282 ms

内存: 16.4 MB

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        points.sort(key=lambda p: (p[0], -p[1]))
        ans = 0
        for i, (_, y0) in enumerate(points):
            min_y = -inf
            for _, y1 in points[i+1:]:
                if min_y < y1 <= y0:
                    min_y = y1
                    ans += 1
        return ans

Explain

解题思路基于排序和迭代搜索的组合。首先，将点按x坐标升序排序，如果x坐标相同，则按y坐标降序排序。这样排序后，对于任意点Alice，所有在其右边的点都是可能的Bob的候选者。接着，遍历每个点作为Alice，对于每个Alice，检查它右边的点作为Bob是否满足条件（即没有其他点在Alice和Bob所形成的矩形区域内）。为了快速判断，使用变量min_y记录遍历过程中遇到的最小y坐标值（即Bob的y坐标必须大于等于这个值，同时小于等于Alice的y坐标），这样可以确保在Alice的右下方的所有点都不会在所形成的矩形内。

时间复杂度: O(n^2)

空间复杂度: O(1)

# Python 代码添加注释版本

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        # 将点按x升序，y降序排序
        points.sort(key=lambda p: (p[0], -p[1]))
        ans = 0
        # 遍历每个点，考虑将其作为Alice的位置
        for i, (_, y0) in enumerate(points):
            min_y = -inf  # 初始化y坐标的最小值
            # 检查当前点右边的所有点作为Bob的位置
            for _, y1 in points[i+1:]:
                # 确保没有其他点在Alice和Bob形成的矩形内部或边缘
                if min_y < y1 <= y0:
                    min_y = y1
                    ans += 1
        return ans

Explore

这样的排序策略有助于简化后续的处理过程。首先，通过x坐标的升序排列，我们可以确保每次处理点Alice时，其右侧的所有点都是潜在的Bob点。其次，当x坐标相同的情况下，通过y坐标的降序排列，我们可以更容易地处理y坐标的比较和限制条件。这样，对于每个Alice点，从该点开始向右遍历时，可以保证之前遇到的点的y坐标都不低于当前处理的点，这有助于维护y坐标的最小值，并有效地判断哪些点能作为合适的Bob。

在遍历可能的Bob点时，`min_y`变量记录了遍历过程中遇到的最小y坐标值。这个最小y坐标值是在Alice点右侧遍历过程中不断更新的。通过设置条件`min_y < y1 <= y0`，我们确保所选的Bob点的y坐标不仅要在Alice点的y坐标以下，还要高于之前遇到的所有其他点的最小y坐标。这样的条件保证了在Alice和Bob之间没有任何其他点的y坐标处于他们所构成的矩形区域内部或边缘，从而确保了矩形区域内的空无性。

题解中的算法假定Alice和Bob的位置不同（即至少在一个坐标方向上有差异），因为算法的目的是寻找能形成有效矩形的点对。如果Alice和Bob的坐标完全相同，实际上无法形成有效的矩形（因为它退化成一条线），且在算法中，这种情况下也不会计数为有效对。因此，在Alice和Bob的坐标完全相同时，这种情况不会被算法考虑为有效的点对。