最大节点价值之和

标签: 贪心 位运算 树 数组 动态规划 排序

难度: Hard

给你一棵 n 个节点的 无向 树，节点从 0 到 n - 1 编号。树以长度为 n - 1 下标从 0 开始的二维整数数组 edges 的形式给你，其中 edges[i] = [ui, vi] 表示树中节点 ui 和 vi 之间有一条边。同时给你一个 正 整数 k 和一个长度为 n 下标从 0 开始的 非负 整数数组 nums ，其中 nums[i] 表示节点 i 的 价值 。

Alice 想 最大化 树中所有节点价值之和。为了实现这一目标，Alice 可以执行以下操作 任意 次（包括 0 次）：

  • 选择连接节点 u 和 v 的边 [u, v] ，并将它们的值更新为：
    • nums[u] = nums[u] XOR k
    • nums[v] = nums[v] XOR k

请你返回 Alice 通过执行以上操作 任意次 后，可以得到所有节点 价值之和 的 最大值 。

示例 1：

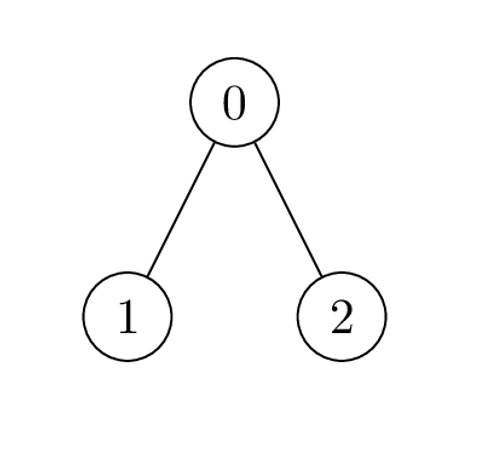
输入：nums = [1,2,1], k = 3, edges = [[0,1],[0,2]]
输出：6
解释：Alice 可以通过一次操作得到最大价值和 6 ：
- 选择边 [0,2] 。nums[0] 和 nums[2] 都变为：1 XOR 3 = 2 ，数组 nums 变为：[1,2,1] -> [2,2,2] 。
所有节点价值之和为 2 + 2 + 2 = 6 。
6 是可以得到最大的价值之和。

示例 2：

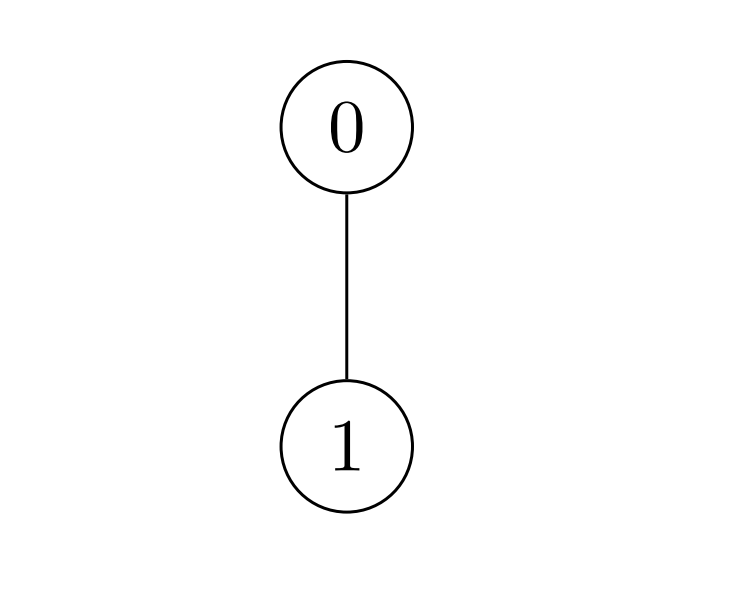
输入：nums = [2,3], k = 7, edges = [[0,1]]
输出：9
解释：Alice 可以通过一次操作得到最大和 9 ：
- 选择边 [0,1] 。nums[0] 变为：2 XOR 7 = 5 ，nums[1] 变为：3 XOR 7 = 4 ，数组 nums 变为：[2,3] -> [5,4] 。
所有节点价值之和为 5 + 4 = 9 。
9 是可以得到最大的价值之和。

示例 3：

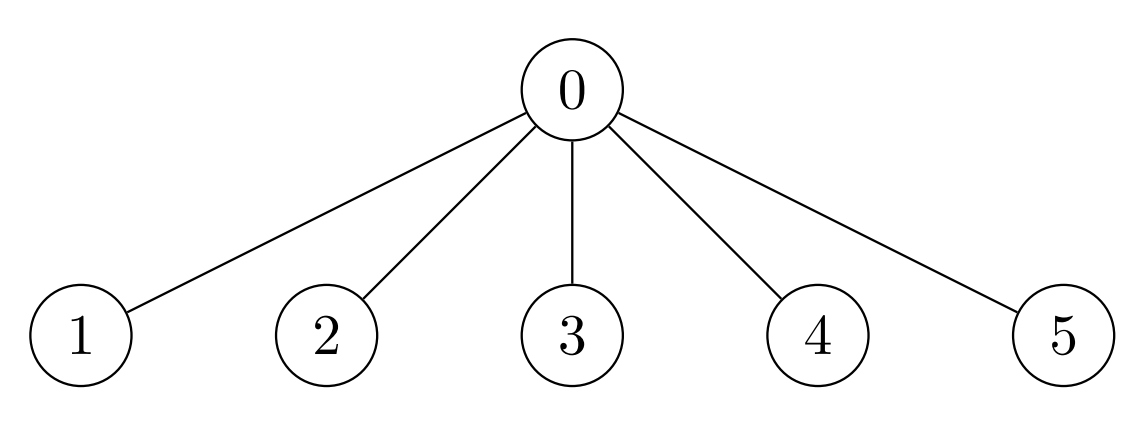
输入：nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]]
输出：42
解释：Alice 不需要执行任何操作，就可以得到最大价值之和 42 。

提示：

  • 2 <= n == nums.length <= 2 * 104
  • 1 <= k <= 109
  • 0 <= nums[i] <= 109
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= edges[i][0], edges[i][1] <= n - 1
  • 输入保证 edges 构成一棵合法的树。

Submission

运行时间: 62 ms

内存: 24.5 MB

class Solution:
    def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:
        n = len(nums)
        s = sum(nums)
        a = []
        b = []
        for x in nums:
            d = (x ^ k) - x
            if d > 0: a.append(d)
            if d <= 0: b.append(d)
        sa = sum(a)
        if len(a) % 2 == 0: return s + sa
        else:
            res = s + sa - min(a)
            if b: res = max(res, s + sa + max(b))
            return res

Explain

此题解采用对每个节点计算XOR操作后与原始值的差值来决定是否进行操作。首先计算整个树节点的初始总价值。然后，对于每个节点，计算执行一次XOR操作后的新价值与原始价值的差值，将所有正差值（代表XOR后价值提高）存储在列表a中，所有非正差值（代表XOR后价值不变或减少）存储在列表b中。如果a的长度是偶数，直接将所有a中的差值加到总价值中即可，因为我们可以选择边来确保执行XOR的次数对于所有提高价值的节点都是偶数次。如果a的长度是奇数，需要移除一个最小的正差值（即最少的价值提升）来使剩余操作次数为偶数，同时也考虑通过执行一次对于价值降低或不变节点的操作来获取可能的最大值。最终，比较这两种策略得到的价值，选择较大的一个。

时间复杂度: O(n)

空间复杂度: O(n)

class Solution:
    def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:
        n = len(nums)
        s = sum(nums)  # 计算原始所有节点价值之和
        a = []  # 存储提高价值的差值
        b = []  # 存储降低或不变的价值差值
        for x in nums:
            d = (x ^ k) - x  # 计算每个节点进行一次XOR后的价值变化
            if d > 0: a.append(d)  # 价值提高，加入列表a
            if d <= 0: b.append(d)  # 价值不提高，加入列表b
        sa = sum(a)  # 计算所有提高的价值总和
        if len(a) % 2 == 0: return s + sa  # 如果提高价值的节点个数为偶数，直接返回总和
        else:
            res = s + sa - min(a)  # 如果为奇数，尝试移除一个最小增加的价值
            if b: res = max(res, s + sa + max(b))  # 考虑通过一次对降低或不变价值的节点的操作获取可能的最大值
            return res

Explore

在题解中计算XOR后的新价值与原始价值的差值而非直接比较新旧价值的大小是为了便于计算总价值的变化量。通过差值，我们可以直接得到每次XOR操作对总价值的具体影响，这样可以更简单地累加或比较这些变化量来决定最终策略。如果直接比较新旧价值，虽然能知道哪个更大，但还需要额外的计算步骤来确定这种变化对整体价值的具体贡献。

将正差值和非正差值分别存储是为了区分哪些节点的价值在XOR操作后会增加（存入列表a），哪些节点的价值不变或减少（存入列表b）。这种分类有助于进行策略决策，尤其是在需要调整操作次数以优化总价值时。列表a中的元素直接关联到总价值的提升，而列表b中的元素则提供了可能的策略调整选项，比如在需要调整操作次数以达到最优结果时，可以考虑从b中选择操作以平衡次数。

在题解中，如果正差值的个数是奇数，则移除一个最小的正差值以使剩余操作次数为偶数的策略是基于最大化总价值的考虑。在树结构中，通过边连接的节点可以通过偶数次XOR操作实现总价值的最大化（因为偶数次XOR操作可以复原到原始值）。若正差值个数为奇数，则至少有一个节点需要进行奇数次XOR操作，这会导致该节点的价值不是最优。因此，移除增加最少的价值可以最小化这种影响，从而使得其他所有提高价值的节点都能通过偶数次操作达到最优状态。此外，还可考虑执行一次对于降低或不变价值的节点的操作，来进一步优化总价值。