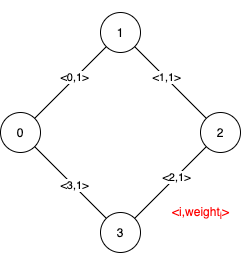
题解使用了并查集和Tarjan算法的结合来解决问题。首先,使用并查集帮助处理并识别最小生成树中的边。通过对边按权重排序,可以便捷地处理同权重的边,使用Tarjan算法来检测关键边(即桥)。算法的核心在于识别出所有权重相同的边组,并在这些组内使用Tarjan算法来查找桥,即关键边。这些关键边是在最小生成树中无法替代的,因此它们是必须的。对于不是桥的边,则标记为伪关键边,表示它们可能在某些最小生成树中出现。
时间复杂度: O(m log m + m α(n) + n + m)
空间复杂度: O(n + m)
# 并查集模板
class UnionFind:
def __init__(self, n: int):
self.parent = list(range(n))
self.size = [1] * n
self.n = n
# 当前连通分量数目
self.setCount = n
def findset(self, x: int) -> int:
if self.parent[x] == x:
return x
self.parent[x] = self.findset(self.parent[x])
return self.parent[x]
def unite(self, x: int, y: int) -> bool:
x, y = self.findset(x), self.findset(y)
if x == y:
return False
if self.size[x] < self.size[y]:
x, y = y, x
self.parent[y] = x
self.size[x] += self.size[y]
self.setCount -= 1
return True
def connected(self, x: int, y: int) -> bool:
x, y = self.findset(x), self.findset(y)
return x == y
# Tarjan 算法求桥边模版
class TarjanSCC:
def __init__(self, n: int, edges: List[List[int]], edgesId: List[List[int]]):
self.n = n
self.edges = edges
self.edgesId = edgesId
self.low = [-1] * n
self.dfn = [-1] * n
self.ans = list()
self.ts = -1
def getCuttingEdge(self) -> List[int]:
for i in range(self.n):
if self.dfn[i] == -1:
self.pGetCuttingEdge(i, -1)
return self.ans
def pGetCuttingEdge(self, u: int, parentEdgeId: int):
self.ts += 1
self.low[u] = self.dfn[u] = self.ts
for v, iden in zip(self.edges[u], self.edgesId[u]):
if self.dfn[v] == -1:
self.pGetCuttingEdge(v, iden)
self.low[u] = min(self.low[u], self.low[v])
if self.low[v] > self.dfn[u]:
self.ans.append(iden)
elif iden != parentEdgeId:
self.low[u] = min(self.low[u], self.dfn[v])
class Solution:
def findCriticalAndPseudoCriticalEdges(self, n: int, edges: List[List[int]]) -> List[List[int]]:
m = len(edges)
for i, edge in enumerate(edges):
edge.append(i)
edges.sort(key=lambda x: x[2])
uf = UnionFind(n)
ans0 = list()
label = [0] * m
i = 0
while i < m:
# 找出所有权值为 w 的边,下标范围为 [i, j)
w = edges[i][2]
j = i
while j < m and edges[j][2] == edges[i][2]:
j += 1
# 存储每个连通分量在图 G 中的编号
compToId = dict()
# 图 G 的节点数
gn = 0
for k in range(i, j):
x = uf.findset(edges[k][0])
y = uf.findset(edges[k][1])
if x != y:
if x not in compToId:
compToId[x] = gn
gn += 1
if y not in compToId:
compToId[y] = gn
gn += 1
else:
# 将自环边标记为 -1
label[edges[k][3]] = -1
# 图 G 的边
gm = collections.defaultdict(list)
gmid = collections.defaultdict(list)
for k in range(i, j):
x = uf.findset(edges[k][0])
y = uf.findset(edges[k][1])
if x != y:
idx, idy = compToId[x], compToId[y]
gm[idx].append(idy)
gmid[idx].append(edges[k][3])
gm[idy].append(idx)
gmid[idy].append(edges[k][3])
bridges = TarjanSCC(gn, gm, gmid).getCuttingEdge()
# 将桥边(关键边)标记为 1
ans0.extend(bridges)
for iden in bridges:
label[iden] = 1
for k in range(i, j):
uf.unite(edges[k][0], edges[k][1])
i = j
# 未标记的边即为非桥边(伪关键边)
ans1 = [i for i in range(m) if label[i] == 0]
return [ans0, ans1]
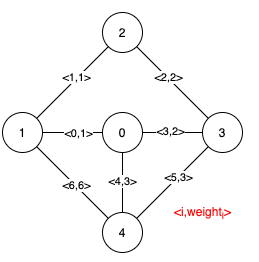
注意到第 0 条边和第 1 条边出现在了所有最小生成树中,所以它们是关键边,我们将这两个下标作为输出的第一个列表。 边 2,3,4 和 5 是所有 MST 的剩余边,所以它们是伪关键边。我们将它们作为输出的第二个列表。