难度: Hard
给定一个数组 trees，其中 trees[i] = [xi, yi] 表示树在花园中的位置。
你被要求用最短长度的绳子把整个花园围起来，因为绳子很贵。只有把 所有的树都围起来，花园才围得很好。
返回恰好位于围栏周边的树木的坐标。
示例 1:
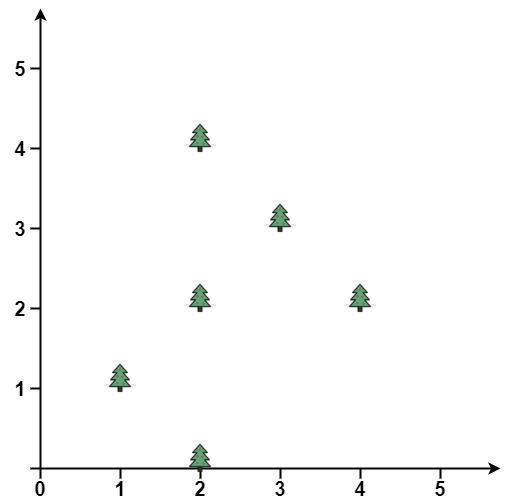
输入: points = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]] 输出: [[1,1],[2,0],[3,3],[2,4],[4,2]]
示例 2:
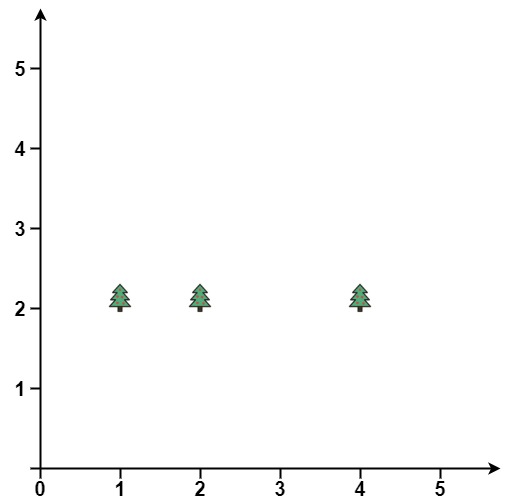
输入: points = [[1,2],[2,2],[4,2]] 输出: [[4,2],[2,2],[1,2]]
注意:
1 <= points.length <= 3000points[i].length == 20 <= xi, yi <= 100所有给定的点都是 唯一 的。
运行时间: 58 ms
内存: 16.6 MB
class Solution:
def outerTrees(self, tree: List[List[int]]) -> List[List[int]]:
trees = [i for i in range(len(tree))]
trees.sort(key=lambda x: tree[x])
# 下凸
down = []
for i in trees:
while len(down) > 1:
x1, y1 = tree[down[-2]]
x2, y2 = tree[down[-1]]
x3, y3 = tree[i]
angle = (x3-x2)*(y1-y2) - (x1-x2)*(y3-y2)
if angle < 0:
down.pop()
else:
break
down.append(i)
# print([tree[i] for i in down])
# trees.sort(key=lambda x: [tree[x][0], -tree[x][1]])
# 上凸
trees.reverse()
up = []
for i in trees:
while len(up) > 1:
x1, y1 = tree[up[-2]]
x2, y2 = tree[up[-1]]
x3, y3 = tree[i]
angle = (x3-x2)*(y1-y2) - (x1-x2)*(y3-y2)
if angle < 0:
up.pop()
else:
break
up.append(i)
vis = set(down) | set(up)
return [tree[i] for i in vis]
该题解使用了凸包算法中的 Andrew 算法。首先将所有点按照 x 坐标排序，如果 x 坐标相同则按 y 坐标排序。然后分别求解点集的上凸壳和下凸壳。对于下凸壳，从左到右遍历每个点，如果当前点与凸壳中最后两个点构成的向量顺时针旋转，则弹出凸壳中的最后一个点，直到当前点与凸壳最后两个点构成的向量不再顺时针旋转，将当前点加入凸壳。上凸壳的求解方法类似，只是需要将点集按照 x 坐标降序排列，然后从右向左遍历每个点。最后将上凸壳和下凸壳求并集即可得到围栏周边的点集。
时间复杂度: O(nlogn)
空间复杂度: O(n)
class Solution:
def outerTrees(self, tree: List[List[int]]) -> List[List[int]]:
# 将点集按照 x 坐标排序，如果 x 坐标相同则按 y 坐标排序
trees = [i for i in range(len(tree))]
trees.sort(key=lambda x: tree[x])
# 求下凸壳
down = []
for i in trees:
while len(down) > 1:
x1, y1 = tree[down[-2]]
x2, y2 = tree[down[-1]]
x3, y3 = tree[i]
# 计算当前点与凸壳最后两个点构成的向量的叉积
angle = (x3-x2)*(y1-y2) - (x1-x2)*(y3-y2)
# 如果叉积小于 0，则当前点与凸壳最后两个点构成的向量顺时针旋转，弹出凸壳的最后一个点
if angle < 0:
down.pop()
else:
break
down.append(i)
# 求上凸壳
trees.reverse() # 将点集按照 x 坐标降序排列
up = []
for i in trees:
while len(up) > 1:
x1, y1 = tree[up[-2]]
x2, y2 = tree[up[-1]]
x3, y3 = tree[i]
# 计算当前点与凸壳最后两个点构成的向量的叉积
angle = (x3-x2)*(y1-y2) - (x1-x2)*(y3-y2)
# 如果叉积小于 0，则当前点与凸壳最后两个点构成的向量顺时针旋转，弹出凸壳的最后一个点
if angle < 0:
up.pop()
else:
break
up.append(i)
# 求上凸壳和下凸壳的并集
vis = set(down) | set(up)
return [tree[i] for i in vis]
在Andrew算法中，判断两个向量是否顺时针旋转可以通过计算这两个向量的叉积来实现。设有三个点A(x1, y1), B(x2, y2)和C(x3, y3)，向量AB由点A指向点B，向量BC由点B指向点C。这两个向量的叉积可以通过以下公式计算：(x2 - x1) * (y3 - y2) - (y2 - y1) * (x3 - x2)。如果此叉积结果为负值，则表示向量AB到BC的转向为顺时针；如果为正，则为逆时针；如果为零，则表示两向量共线。
在求上凸壳时，将点集按照x坐标降序排列的目的是为了简化算法的实现。这样排序后，可以使用与求下凸壳相似的逻辑从右向左遍历点集，这使得在检查和处理每个新点时，可以重用与求下凸壳相同的叉积逻辑。这种排序保证了在遍历点时，我们总是在处理当前凸壳的“外侧”，从而可以有效地构建凸壳。
当算法遇到平行于x轴或y轴的边界情况时，即当向量的叉积结果为零时，表示两个向量共线。在Andrew算法中，通常会选择将这些共线的点都包括在凸壳中。这是因为这些点在数学上都位于同一直线上，且在实际应用中（如建立围栏），可能需要包括所有边界上的点。具体实现时，算法会在检测到叉积为零时继续将当前点加入凸壳，而不是排除它。
每个点在上下凸壳的求解过程中最多被弹出一次的保证，与算法的单调性和排序有关。首先，由于点集已被按x坐标（及必要时按y坐标）排序，每个点都会按序被处理。当一个点被加入凸壳后，只有在发现新的点导致向量顺时针转动时，该点才可能被弹出。一旦一个点被弹出，由于点的顺序处理和向量叉积的性质，该点不会再次进入考虑队列，因此每个点最多只被弹出一次。这样的操作保证了算法的效率和正确性。