查询树中环的长度

标签: 树二叉树

难度: Hard

给你一个整数 n ，表示你有一棵含有 2ⁿ - 1 个节点的 完全二叉树 。根节点的编号是 1 ，树中编号在[1, 2^{n - 1} - 1] 之间，编号为 val 的节点都有两个子节点，满足：

左子节点的编号为 2 * val
右子节点的编号为 2 * val + 1

给你一个长度为 m 的查询数组 queries ，它是一个二维整数数组，其中 queries[i] = [a_i, b_i] 。对于每个查询，求出以下问题的解：

在节点编号为 a_i 和 b_i 之间添加一条边。
求出图中环的长度。
删除节点编号为 a_i 和 b_i 之间新添加的边。

注意：

环是开始和结束于同一节点的一条路径，路径中每条边都只会被访问一次。
环的长度是环中边的数目。
在树中添加额外的边后，两个点之间可能会有多条边。

请你返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 个查询的结果。

示例 1：

输入：n = 3, queries = [[5,3],[4,7],[2,3]]
输出：[4,5,3]
解释：上图是一棵有 2³ - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 3 和节点 5 之间添加边后，环为 [5,2,1,3] ，所以第一个查询的结果是 4 。删掉添加的边后处理下一个查询。
- 在节点 4 和节点 7 之间添加边后，环为 [4,2,1,3,7] ，所以第二个查询的结果是 5 。删掉添加的边后处理下一个查询。
- 在节点 2 和节点 3 之间添加边后，环为 [2,1,3] ，所以第三个查询的结果是 3 。删掉添加的边。

示例 2：

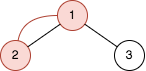
输入：n = 2, queries = [[1,2]]
输出：[2]
解释：上图是一棵有 2² - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 1 和节点 2 之间添加边后，环为 [2,1] ，所以第一个查询的结果是 2 。删掉添加的边。

提示：

2 <= n <= 30
m == queries.length
1 <= m <= 10⁵
queries[i].length == 2
1 <= a_i, b_i <= 2ⁿ - 1
a_i != b_i

Submission

运行时间: 91 ms

内存: 45.9 MB

class Solution:
    def cycleLengthQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        res = [1] * len(queries)
        for i,(a,b) in enumerate(queries):
            if a < b:
                a, b = b, a
            l = a.bit_length() - b.bit_length()
            res[i] += l + 2 * ((a >> l) ^ b).bit_length()
        return res

Explain

这个题解利用了完全二叉树的性质和位运算来找到从一个节点到另一个节点的路径。对于每个查询，首先确定两个节点中的较大值作为a，较小值作为b。然后计算a和b的二进制表示的长度差，这个长度差l代表了a相对于b在树中的深度差。接下来，通过右移操作将a移动到与b相同的深度，然后通过异或操作计算这两个同深度的节点的差异。这个差异的二进制表示中的1的个数表示了在同一层内，从一个节点到另一个节点需要经过的节点数。环的长度是由从a到b的路径长度加上额外的一条边组成的，因此总长度是a到b同层路径长度的两倍加上从a降到b的层的长度l再加上1（代表新增的边）。

时间复杂度: O(m)

空间复杂度: O(1)

class Solution:
    def cycleLengthQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        res = [1] * len(queries)  # 初始化结果数组，每个查询至少包含一条额外的边
        for i, (a, b) in enumerate(queries):  # 遍历所有查询
            if a < b:  # 确保a是较大的一个
                a, b = b, a
            l = a.bit_length() - b.bit_length()  # 计算深度差
            res[i] += l + 2 * ((a >> l) ^ b).bit_length()  # 计算环的长度
        return res

Explore

确保a是较大的值可以简化路径计算的逻辑。在完全二叉树中，任何节点的父节点的值都比它小。如果a始终是较大的值，可以直接通过右移操作（即除以2的操作）计算a向上移动到与b相同深度的路径。如果b是较大的值，则需要额外的逻辑来处理这种情况，因此统一a为较大值可以使算法更简洁，易于理解。

异或操作用于找出两个数在二进制形式下的不同位，每个不同的位代表这两个节点在该位上的路径选择不同（一个选择左子树，一个选择右子树）。因此，异或结果中1的个数表示在同一层内，两个节点在路径上的差异点数量，即需要经过的额外节点数。这种方法直接反映了两个节点在同一层内的距离。

深度差l是通过计算两个数的二进制表示的长度差得到的。右移操作（即`a >> l`）实质上是将a的二进制表示向右移动l位，这相当于在完全二叉树中将节点a向上移动l层，使其达到与节点b相同的深度。这种方法在完全二叉树的结构下是有效的，因为树的每一层的节点数都是上一层的两倍，节点的值也是按顺序分配的。

将同层路径长度乘以两倍是因为环的计算需要考虑从a到b的路径和再从b回到a的路径。即便是在树结构中，环的形成意味着路径必须回到起点，因此计算总路径时，同层内从a到b的距离需要走两次：一次从a到b，一次从b回到a。