统计完全连通分量的数量

难度: Medium

给你一个整数 n 。现有一个包含 n 个顶点的无向图，顶点按从 0 到 n - 1 编号。给你一个二维整数数组 edges 其中 edges[i] = [a_i, b_i] 表示顶点 a_i 和 b_i 之间存在一条无向边。

返回图中 完全连通分量 的数量。

如果在子图中任意两个顶点之间都存在路径，并且子图中没有任何一个顶点与子图外部的顶点共享边，则称其为 连通分量 。

如果连通分量中每对节点之间都存在一条边，则称其为 完全连通分量 。

示例 1：

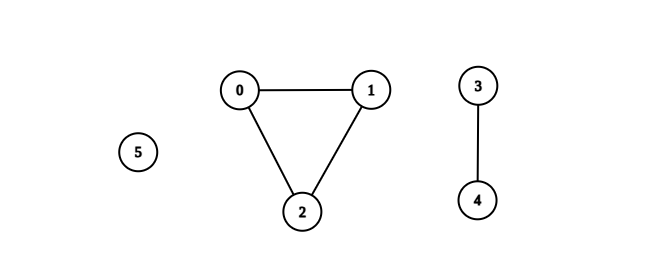
输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
输出：3
解释：如上图所示，可以看到此图所有分量都是完全连通分量。

示例 2：

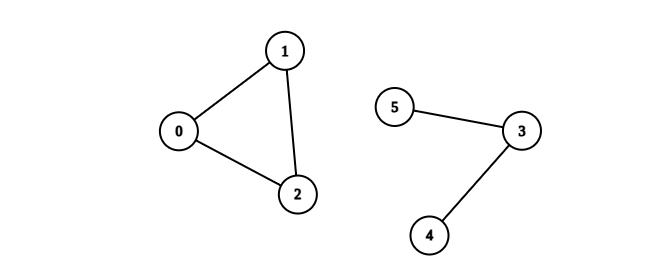
输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
输出：1
解释：包含节点 0、1 和 2 的分量是完全连通分量，因为每对节点之间都存在一条边。
包含节点 3 、4 和 5 的分量不是完全连通分量，因为节点 4 和 5 之间不存在边。
因此，在图中完全连接分量的数量是 1 。

提示：

1 <= n <= 50
0 <= edges.length <= n * (n - 1) / 2
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
不存在重复的边

Submission

运行时间: 74 ms

内存: 16.5 MB

class Solution:
    def countCompleteComponents(self, n: int, edges: List[List[int]]) -> int:
        graph = [[] for _ in range(n)]
        for vertex1, vertex2 in edges:
            graph[vertex1].append(vertex2)
            graph[vertex2].append(vertex1)
        connected_set = []  # 统计每个联通分量中的顶点和边数目
        
        ans = 0
        visited_vertex = set()
        for i in range(n):
            if i not in visited_vertex:
                vertex_num = 0
                edge_num = 0  # 统计的为原本的2倍
                visited_vertex.add(i)

                queue = deque()
                queue.append(i)
                while queue:
                    cur_vertex = queue.popleft()
                    vertex_num += 1
                    edge_num += len(graph[cur_vertex])
                    for nxt_vertex in graph[cur_vertex]:
                        if nxt_vertex not in visited_vertex:
                            queue.append(nxt_vertex)
                            visited_vertex.add(nxt_vertex)
                
                if vertex_num * (vertex_num - 1) == edge_num:  # 故左边不需要除以2
                    ans += 1
        
        return ans

Explain

此题解采用的是广度优先搜索(BFS)来遍历图中的每个顶点，并同时记录每个连通分量中的顶点数(vertex_num)和边数的两倍(edge_num)。首先，构建了图的邻接表表示。然后，对于每个未访问的顶点，使用BFS来遍历其所在的连通分量，记录下顶点数和边数的两倍。在BFS过程中，每次从队列中取出一个顶点，增加顶点数，增加的边数为该顶点连接的边数（注意这里边数会被计算两次，即每条边的两个顶点各计一次）。最后，检查该连通分量是否为完全连通分量，即顶点数(vertex_num)和边数(edge_num)之间的关系是否符合完全图的性质（完全图的边数为顶点数 * (顶点数 - 1) / 2，因为边数edge_num统计了两次，因此直接比较vertex_num * (vertex_num - 1)和edge_num是否相等）。如果相等，说明是完全连通分量，答案加一。

时间复杂度: O(V + E)

空间复杂度: O(V + E)

class Solution:
    def countCompleteComponents(self, n: int, edges: List[List[int]]) -> int:
        graph = [[] for _ in range(n)]  # 创建邻接表
        for vertex1, vertex2 in edges:
            graph[vertex1].append(vertex2)
            graph[vertex2].append(vertex1)
        ans = 0
        visited_vertex = set()  # 记录已访问的顶点
        for i in range(n):
            if i not in visited_vertex:
                vertex_num = 0
                edge_num = 0  # 初始化顶点数和边数(记为两倍)
                visited_vertex.add(i)
                queue = deque()
                queue.append(i)  # BFS开始
                while queue:
                    cur_vertex = queue.popleft()
                    vertex_num += 1
                    edge_num += len(graph[cur_vertex])
                    for nxt_vertex in graph[cur_vertex]:
                        if nxt_vertex not in visited_vertex:
                            queue.append(nxt_vertex)
                            visited_vertex.add(nxt_vertex)
                if vertex_num * (vertex_num - 1) == edge_num:  # 检查是否为完全连通分量
                    ans += 1
        return ans

Explore

在算法中，每条边在两个顶点之间形成连接，所以在遍历过程中，每条边会被两次计算（一次从每个端点）。例如，若边连接顶点A和B，则在遍历A时记录这条边，同样在遍历B时也会记录这条边。这样做可以简化边计数的过程，确保每条边被完全考虑，同时也便于后续判断完全连通分量时直接使用乘以二的边数进行计算，而不用再除以二去还原实际的边数。

完全图的定义是图中的每对不同顶点之间都恰好有一条边。因此，一个包含n个顶点的完全图中的边数是n*(n-1)/2，因为每个顶点与其他n-1个顶点相连，并且每条边只计算一次。在本算法中，由于每条边在计算时被计数了两次（一次从每个顶点），因此实际边数的两倍就是vertex_num * (vertex_num - 1)。比较这个值与edge_num是否相等可以直接判断该连通分量是否为完全连通分量。

是的，如果图中存在自环或多重边，则当前算法可能会产生错误的结果，因为自环会增加边数但不会增加额外的顶点间连接，多重边同样会错误地增加边的计数。为了适应这些情况，算法需要调整以正确处理自环和多重边：可以在构建图的邻接表时忽略自环，并且只存储唯一的边。这通常通过使用集合（而不是列表）来存储与每个顶点相连的其他顶点来实现，从而自动去除重复的条目。

在BFS过程中，一旦访问一个顶点，立即将其加入到已访问集合中是为了防止该顶点被重复访问和排队。这个做法可以防止在队列中重复添加相同的顶点，从而避免不必要的重复工作和可能的无限循环。此外，这样做可以确保每个顶点和与之相关的边只被处理一次，有效保持算法的正确性和效率。