难度: Medium
给你一个 m x n 的二进制矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。
示例 1：
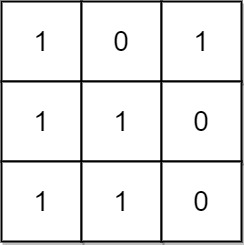
输入：mat = [[1,0,1],[1,1,0],[1,1,0]] 输出：13 解释： 有 6 个 1x1 的矩形。 有 2 个 1x2 的矩形。 有 3 个 2x1 的矩形。 有 1 个 2x2 的矩形。 有 1 个 3x1 的矩形。 矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
示例 2：
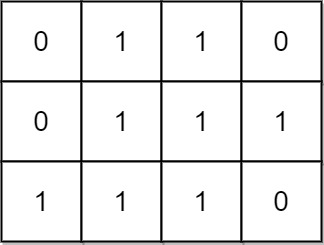
输入：mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] 输出：24 解释： 有 8 个 1x1 的子矩形。 有 5 个 1x2 的子矩形。 有 2 个 1x3 的子矩形。 有 4 个 2x1 的子矩形。 有 2 个 2x2 的子矩形。 有 2 个 3x1 的子矩形。 有 1 个 3x2 的子矩形。 矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。
提示：
1 <= m, n <= 150mat[i][j] 仅包含 0 或 1运行时间: 68 ms
内存: 16.9 MB
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
pre = [0] * (n + 1)
ans = 0
for i in range(m):
dp = [0] * n
stack = [-1]
for j in range(n):
pre[j] = pre[j] + 1 if mat[i][j] == 1 else 0
while pre[stack[-1]] > pre[j]:
stack.pop()
dp[j] = dp[stack[-1]] + pre[j] * (j - stack[-1])
stack.append(j)
ans += sum(dp)
return ans
本题解使用动态规划和单调栈的方法来计算所有全1子矩形的数量。首先，定义一个'pre'数组来保存当前列中连续1的数量，每次遇到1时在前一个基础上加1，遇到0则重置为0。接着，使用动态规划数组'dp'来计算以每个位置为底的所有可能的全1子矩形的数量。具体地，通过维护一个单调栈来快速找到当前列之前的较小值位置，并根据这个位置更新当前位置的'dp'值。'dp[j]'表示在第i行中，以第j列为右下角的矩形数量。最后，将所有行的'dp'值累加得到最终答案。
时间复杂度: O(m * n)
空间复杂度: O(n)
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0]) # 获取矩阵的行数和列数
pre = [0] * (n + 1) # 初始化前缀和数组，用于计算每列连续1的数量
ans = 0 # 初始化结果变量
for i in range(m): # 遍历每一行
dp = [0] * n # 初始化当前行的dp数组
stack = [-1] # 初始化单调栈，用于记录列索引
for j in range(n): # 遍历当前行的每一列
pre[j] = pre[j] + 1 if mat[i][j] == 1 else 0 # 更新连续1的数量
while pre[stack[-1]] > pre[j]: # 维护单调递增栈
stack.pop() # 弹出栈顶元素
dp[j] = dp[stack[-1]] + pre[j] * (j - stack[-1]) # 计算以mat[i][j]为右下角的子矩形数量
stack.append(j) # 将当前列索引压入栈
ans += sum(dp) # 将当前行的子矩形数量加到总数中
return ans # 返回结果
在动态规划中使用单调栈来维护列索引，是为了快速找到每个元素左边和右边第一个小于当前元素的位置，这种方法广泛应用于处理类似直方图的问题。单调栈能够帮助我们维护一个递增或递减的序列，从而在O(n)时间复杂度内解决问题。在这个题目中，单调栈用于维护一个递增的栈，这样可以快速确定每个位置左侧连续1的最大可能扩展范围，从而高效计算每个位置作为右下角时的子矩形数量。
这个状态转移方程的含义是计算以当前位置为右下角的所有全1子矩形的数量。`dp[stack[-1]]`表示之前(即栈顶元素指向的位置)已计算的矩形数量。而`pre[j] * (j - stack[-1])`部分表示当前列高度为`pre[j]`的矩形数量，乘以这种高度矩形从栈顶元素到当前位置j的宽度`(j - stack[-1])`。这样，我们就可以将从栈顶位置到当前位置的所有以`pre[j]`为高的矩形数量加上之前的数量，得到以当前位置为右下角的矩形总数。
`pre`数组用于记录每一列连续的1的数量。这是因为只有连续的1才能构成子矩形。如果在某一列中间有0出现，那么它上面的所有1都不能与它下面的1形成更大的矩形。通过维护`pre`数组，我们可以快速知道到当前行为止，每一列最多能向上扩展多少行，这是计算全1子矩形不可或缺的信息。
这里的逻辑是为了保证栈中维持的是一个递增的序列。在栈中，每个元素都代表一个高度，且栈顶元素是最近的一个比当前高度小的值。当当前列的高度`pre[j]`小于栈顶列的高度`pre[stack[-1]]`时，意味着栈顶元素不能作为当前矩形的边界（因为它比当前要高，会阻断当前高度的扩展），因此需要将其移除。这样可以保证每个矩形的右边界是正确的，且计算的子矩形数量是准确的。