统计圆内格点数目

难度: Medium

给你一个二维整数数组 circles ，其中 circles[i] = [x_i, y_i, r_i] 表示网格上圆心为 (x_i, y_i) 且半径为 r_i 的第 i 个圆，返回出现在 至少一个 圆内的 格点数目 。

注意：

格点是指整数坐标对应的点。
圆周上的点 也被视为出现在圆内的点。

示例 1：

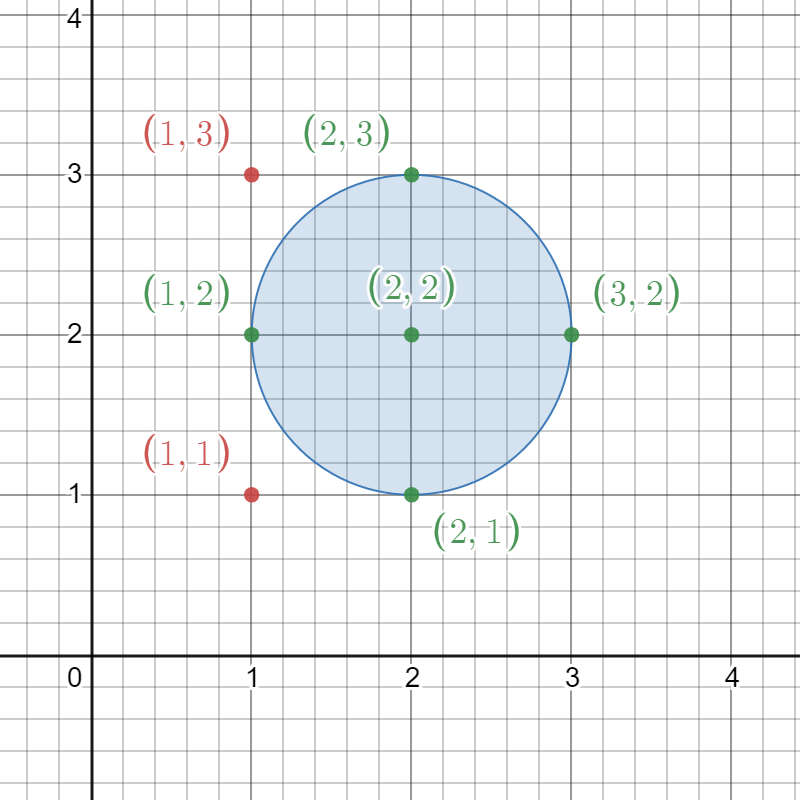
输入：circles = [[2,2,1]]
输出：5
解释：
给定的圆如上图所示。
出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2)，在图中用绿色标识。
像 (1, 1) 和 (1, 3) 这样用红色标识的点，并未出现在圆内。
因此，出现在至少一个圆内的格点数目是 5 。

示例 2：

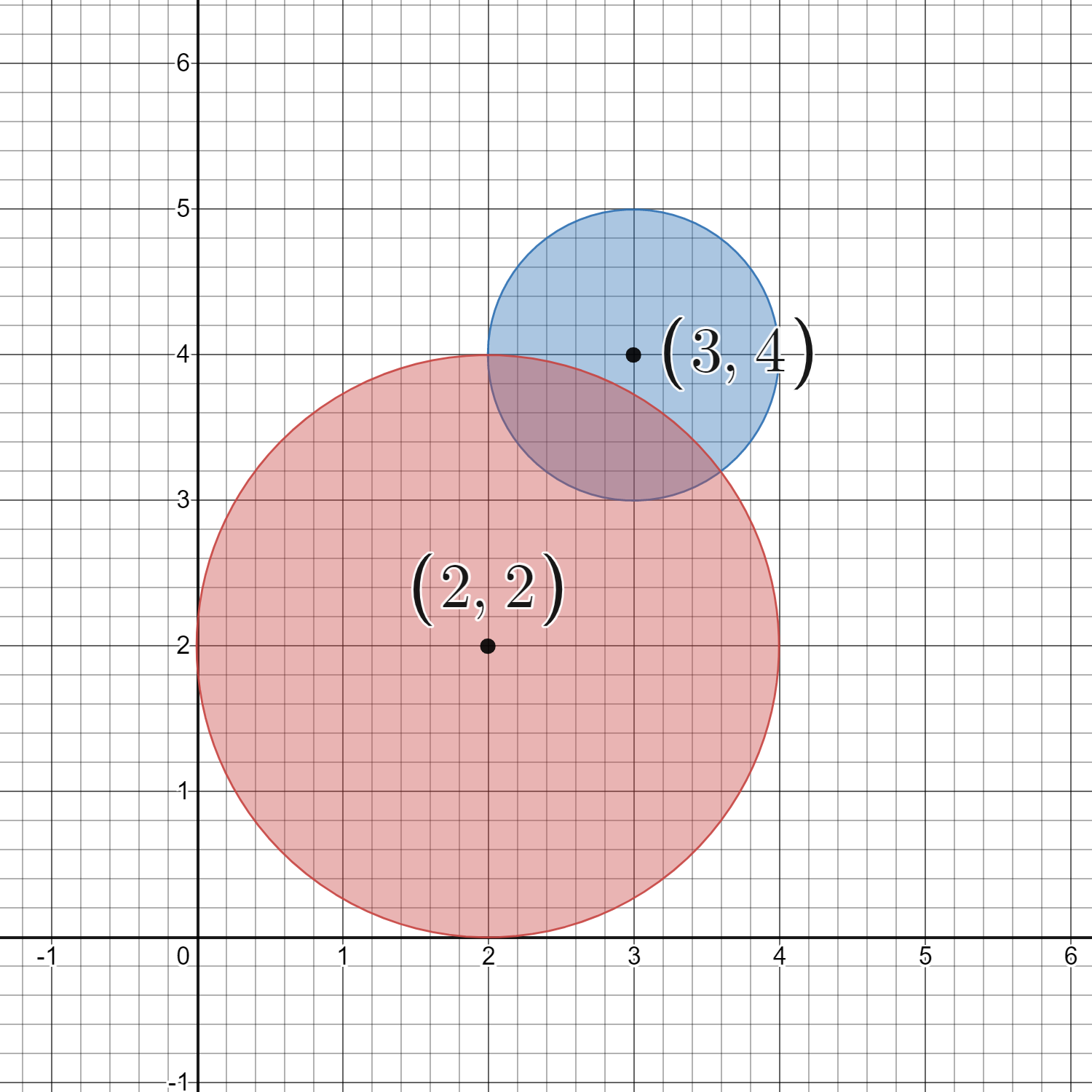
输入：circles = [[2,2,2],[3,4,1]]
输出：16
解释：
给定的圆如上图所示。
共有 16 个格点出现在至少一个圆内。
其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4) 。

提示：

1 <= circles.length <= 200
circles[i].length == 3
1 <= x_i, y_i <= 100
1 <= r_i <= min(x_i, y_i)

Submission

运行时间: 53 ms

内存: 16.4 MB

class Solution:
    def countLatticePoints(self, circles: List[List[int]]) -> int:
        mx, my = max(cx + cr for cx, cy, cr in circles) + 2, max(cy + cr for cx, cy, cr in circles) + 1
        diffs = [[0] * mx for _ in range(my)]
        for cx, cy, cr in circles:
            for y in range(cy - cr, cy + cr + 1):
                z = isqrt(cr * cr - (y - cy) ** 2)
                diffs[y][cx - z] += 1
                diffs[y][cx + z + 1] -= 1
        return sum(sum(cur > 0 for cur in accumulate(xs)) for xs in diffs)

Explain

此题解采用了差分数组和积分图的思想来计算网格中的格点数。首先，确定一个足够大的矩形区域来包含所有的圆。然后，对于每个圆，计算其横跨的所有行，并在每行的起始和结束位置进行标记，使用差分的方法记录进入圆和离开圆的点。最后，通过累积这些差分值来确定每个点是否在至少一个圆内，进而统计总的格点数目。

时间复杂度: O(n * r + X * Y)

空间复杂度: O(X * Y)

class Solution:
    def countLatticePoints(self, circles: List[List[int]]) -> int:
        # 计算需要覆盖的最大x和y范围
        mx, my = max(cx + cr for cx, cy, cr in circles) + 2, max(cy + cr for cx, cy, cr in circles) + 1
        # 创建差分数组
        diffs = [[0] * mx for _ in range(my)]
        for cx, cy, cr in circles:
            for y in range(cy - cr, cy + cr + 1):
                z = isqrt(cr * cr - (y - cy) ** 2)
                diffs[y][cx - z] += 1
                diffs[y][cx + z + 1] -= 1
        # 计算累积值并统计结果
        return sum(sum(cur > 0 for cur in accumulate(xs)) for xs in diffs)

Explore

使用差分数组和积分图的方法可以显著提高算法效率。在传统的遍历所有网格点的方法中，我们需要对每个网格点检查其是否位于任一圆内，这在圆的数量或网格的规模很大时非常耗时。而差分数组使得我们只需对每个圆影响的区域边界进行操作，然后通过简单的一次遍历来构建整个区域的覆盖情况，从而降低了时间复杂度。这种方法特别适用于处理大规模数据，能够有效地减少计算量和提高性能。

为了确定包含所有圆的矩形区域大小，我们首先需要找出所有圆的最远边界。具体来说，我们计算所有圆心加上其半径得到的最大x和最大y值（即每个圆的最右侧和最上侧位置），然后再分别在这些值的基础上增加一定的边界（例如加1或加2），以确保整个圆都被包含在内。这样计算出的矩形区域保证可以覆盖所有的输入圆。

此公式是基于圆的方程(x - cx)^2 + (y - cy)^2 = cr^2来计算的。在确定圆在某一行y的横跨范围时，我们固定y值，解出x值。将圆的方程改写为x的形式，x = sqrt(cr^2 - (y - cy)^2) + cx。这里，isqrt是整数平方根函数，用于确保结果为整数，这对于网格点计算来说是必要的。计算出x的范围后，我们就得到了圆在该行的横跨范围，即从(cx - z)到(cx + z)。

差分数组的工作原理是通过记录每个区间的开始和结束来快速计算区间内的累积值。当我们在`cx - z`处加1时，表示从这个点开始，圆开始覆盖这一段区域。而在`cx + z + 1`处减1的目的是表示圆在`cx + z`结束覆盖，因此需要在其后一个位置减去1，以确保只在圆的实际覆盖范围内计算覆盖次数。这样，当我们对差分数组进行累积求和时，每个被圆覆盖的点都会被正确计算，而圆外的点则不会被错误地包括。