有向无环图中一个节点的所有祖先

标签: 深度优先搜索 广度优先搜索 图 拓扑排序

难度: Medium

给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。

给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。

请你返回一个数组 answer，其中 answer[i]是第 i 个节点的所有 祖先 ，这些祖先节点 升序 排序。

如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的 祖先 节点。

示例 1：

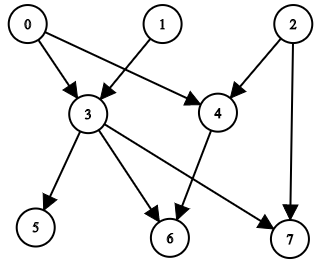
输入：n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出：[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 ，1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ，1 和 3 。
- 节点 6 有 5 个祖先 0 ，1 ，2 ，3 和 4 。
- 节点 7 有 4 个祖先 0 ，1 ，2 和 3 。

示例 2：

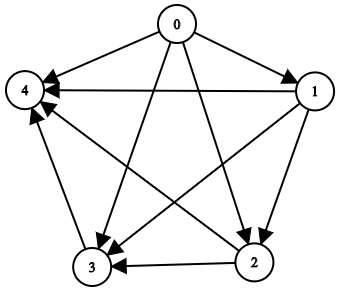
输入：n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
输出：[[],[0],[0,1],[0,1,2],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 没有任何祖先。
- 节点 1 有 1 个祖先 0 。
- 节点 2 有 2 个祖先 0 和 1 。
- 节点 3 有 3 个祖先 0 ，1 和 2 。
- 节点 4 有 4 个祖先 0 ，1 ，2 和 3 。

提示：

  • 1 <= n <= 1000
  • 0 <= edges.length <= min(2000, n * (n - 1) / 2)
  • edges[i].length == 2
  • 0 <= fromi, toi <= n - 1
  • fromi != toi
  • 图中不会有重边。
  • 图是 有向 且 无环 的。

Submission

运行时间: 88 ms

内存: 46.4 MB

class Solution:
    def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        # 有向图求节点祖先可考虑反向建图,路径上的点都是祖先
        # 入度为0的点为根节点，开始遍历。
        # dfs过程中会有重复遍历多个节点的情况，采用记忆化搜索
        # ps:这一题用拓扑排序更好写

        nodein=[0]*n
        ans=[set()for _ in range(n)];e=[[]for _ in range(n)]
        for a,b in edges:
            e[a].append(b)      # 拓扑排序时正向建图
            nodein[b]+=1

        #拓扑排序（本质是bfs）
        q=deque()
        for i in range(n):
            if nodein[i]==0:q.append(i)
        
        while q:
            node=q.pop()
            for j in e[node]:
                nodein[j]-=1
                if nodein[j]==0:q.append(j)
                ans[j]|=ans[node];ans[j].add(node)
                
        return [sorted(x) for x in ans]



        '''
        @cache
        def dfs(i):
            res={i}
            for j in e[i]:
                res=res|dfs(j)
            return res
        
        for i in range(n):
            node_ans=dfs(i).copy()
            node_ans.remove(i)
            ans.append(sorted(node_ans))
        return ans
        '''

Explain

此题解使用了拓扑排序的方法来解决有向无环图中查找所有节点的祖先问题。首先，通过遍历边列表构建每个节点的出度表和记录每个节点的入度。然后，使用队列进行拓扑排序，队列初始包含所有入度为0的节点（即没有任何祖先的节点）。在拓扑排序过程中，每次从队列中取出一个节点，并将其所有直接后继的入度减1。如果后继节点的入度变为0，意味着已经处理了该节点的所有前驱节点，将其加入队列继续处理。同时，更新后继节点的祖先集合，将当前节点及其祖先集合并入后继节点的祖先集合。最终，对每个节点的祖先集合进行排序后输出。

时间复杂度: O(V^2 log V)

空间复杂度: O(V^2)

class Solution:
    def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        # 初始化入度数组和邻接表
        nodein = [0] * n
        ans = [set() for _ in range(n)]
        e = [[] for _ in range(n)]
        for a, b in edges:
            e[a].append(b)  # 构建正向邻接表
            nodein[b] += 1  # 记录入度

        # 使用队列进行拓扑排序
        q = deque()
        for i in range(n):
            if nodein[i] == 0: q.append(i)

        while q:
            node = q.pop()
            for j in e[node]:
                nodein[j] -= 1
                if nodein[j] == 0: q.append(j)
                ans[j] |= ans[node]
                ans[j].add(node)

        # 对每个节点的祖先集合进行排序
        return [sorted(x) for x in ans]

Explore

构建每个节点的入度表和邻接表对于实现拓扑排序至关重要。入度表记录每个节点被多少其他节点指向，这有助于确定没有任何前驱（即入度为0的节点），可以作为拓扑排序的起始点。邻接表则记录了每个节点指向的其他节点，这样在进行拓扑排序时，可以轻松找到节点的所有直接后继。使用这些结构，可以有效地管理和更新图中节点的状态，同时确保整个拓扑排序过程的正确性和效率。

在拓扑排序中使用队列而非栈，是为了保证节点按照从入度为0的节点开始的顺序被处理。队列是一种先进先出（FIFO）的数据结构，确保了最早加入队列的节点（即最早变为无前驱的节点）最先被处理。这有助于顺序地解决节点的依赖关系，使得每个节点在其所有前驱节点都已被处理后才被处理，从而保持了拓扑排序的正确性。如果使用栈（后进先出），则可能导致依赖关系的处理顺序混乱，影响排序结果的有效性。

在拓扑排序中，当一个节点从队列中取出时，表示其所有前驱节点已经被处理，因此它的祖先集合是已知的。将该节点的祖先集合传递给其所有直接后继节点并添加当前节点到后继的祖先集合中，是为了确保后继节点在处理时，能够累积所有其祖先的信息。这种传递和更新祖先信息的方法，保证了在整个拓扑排序结束时，每个节点的祖先集合完整且正确地反映了所有可能的祖先路径。

对于完全没有连接的孤立节点，它们在拓扑排序的入度表中的值为0，因为没有任何节点指向它们。在实现拓扑排序时，这些节点会在初始阶段被添加到队列中，因为它们的入度为0。在处理这些节点时，由于它们没有前驱也没有后继，它们的祖先集合将保持为空。因此，孤立节点在排序和祖先的处理上不会引起任何问题，它们会自然地按照算法的逻辑被正确处理。