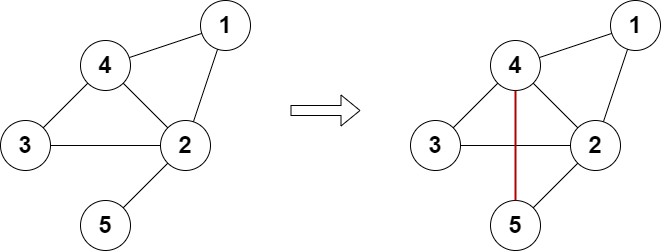
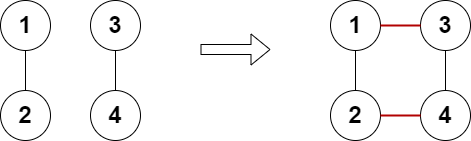
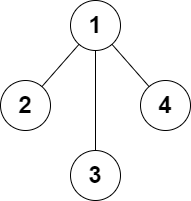
这个题解的思路是首先统计每个节点的度数,然后根据度数的奇偶性来判断是否可以通过添加边使得所有节点的度数都变为偶数。具体来说,如果某个节点的度数等于n-1且为奇数,则无法通过添加边使其变为偶数,直接返回False。然后将所有度数为奇数的节点收集起来,如果奇数节点的个数大于4或为奇数,则无法通过添加边使得所有节点的度数都变为偶数,返回False。如果没有奇数节点,则不需要添加边,返回True。如果有两个奇数节点,检查是否可以通过添加一条边使得这两个节点的度数都变为偶数。如果有四个奇数节点,检查是否可以通过添加两条边使得这四个节点的度数都变为偶数。
时间复杂度: O(m+n)
空间复杂度: O(n)
class Solution:
def isPossible(self, n: int, edges: List[List[int]]) -> bool:
m = len(edges)
count = {}
for i in range(m):
u, v = edges[i][0], edges[i][1]
count[u] = count.get(u, 0) + 1
count[v] = count.get(v, 0) + 1
odd = []
for k in count:
if count[k] == n-1 and count[k] % 2 == 1:
return False
elif count[k] % 2 == 1:
odd.append(k)
if len(odd) > 4 or len(odd) % 2 == 1:
return False
if len(odd) == 0:
return True
elif len(odd) == 2:
if not [odd[0], odd[1]] in edges and not [odd[1], odd[0]] in edges:
return True
for i in range(1,n+1):
if i in odd:
continue
else:
if not [odd[0], i] in edges and not [i, odd[0]] in edges and \
not [odd[1], i] in edges and not [i, odd[1]] in edges:
return True
return False
else:
for i in range(1, 4):
a = [odd[0], odd[i]]
b = [odd[j] for j in range(1,4) if odd[j] not in a]
if not [a[0], a[1]] in edges and not [a[1], a[0]] in edges and \
not [b[0], b[1]] in edges and not [b[1], b[0]] in edges:
return True
return False